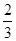题目内容
已知圆P:x2+y2=4y及抛物线S:x2=8y,过圆心P作直线l,此直线与上述两曲线的四个交点,自左向右顺次记为A,B,C,D,如果线段AB,BC,CD的长按此顺序构成一个等差数列,则直线l的斜率为( )
A.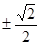 | B.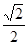 | C.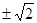 | D.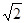 |
A
解析试题分析:圆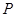 的方程为
的方程为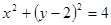 ,则其直径长
,则其直径长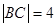
圆心为 ,设
,设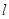 的方程为
的方程为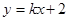 ,代入抛物线方程得:
,代入抛物线方程得: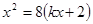
设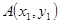 ,
,
有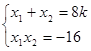
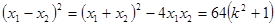
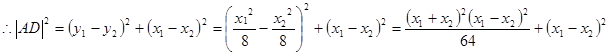
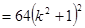
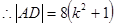
∴线段 的长按此顺序构成一个等差数列,
的长按此顺序构成一个等差数列,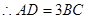 ,即
,即 ,解得
,解得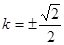 ,故选A.
,故选A.
考点:1.抛物线的几何性质;2.直线与抛物线相交问题.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知双曲线C的离心率为2,焦点为 、
、 ,点A在C上,若
,点A在C上,若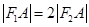 ,则
,则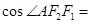 ( )
( )
A. | B.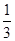 | C. | D.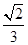 |
(5分)(2011•湖北)将两个顶点在抛物线y2=2px(p>0)上,另一个顶点是此抛物线焦点的正三角形个数记为n,则( )
| A.n=0 | B.n=1 | C.n=2 | D.n≥3 |
已知双曲线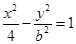 的右焦点与抛物线
的右焦点与抛物线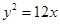 的焦点重合,则该双曲线的焦点到其渐近线的距离等于( ).
的焦点重合,则该双曲线的焦点到其渐近线的距离等于( ).
A.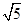 | B.4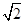 | C.3 | D.5 |
若双曲线 -
- =1(a>0,b>0)上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为( )
=1(a>0,b>0)上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为( )
A.(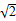 ,+∞) ,+∞) | B.[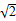 ,+∞) ,+∞) |
C.(1,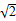 ] ] | D.(1,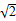 ) ) |
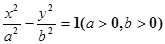 的左、右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线的某条渐近线于M、N两点,且满足
的左、右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线的某条渐近线于M、N两点,且满足 MAN=120o,则该双曲线的离心率为( )
MAN=120o,则该双曲线的离心率为( )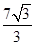
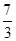
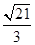
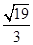
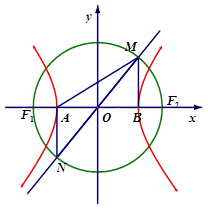
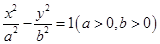 的左、右焦点分别为
的左、右焦点分别为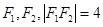 ,P是双曲线右支上的一点,
,P是双曲线右支上的一点,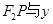 轴交于点A,
轴交于点A,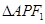 的内切圆在
的内切圆在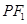 上的切点为Q,若
上的切点为Q,若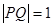 ,则双曲线的离心率是
,则双曲线的离心率是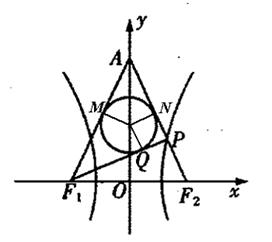
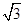
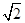
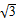
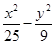 =1的左支上一点M到右焦点F2的距离为18,N是线段MF2的中点,O是坐标原点,则|ON|等于( )
=1的左支上一点M到右焦点F2的距离为18,N是线段MF2的中点,O是坐标原点,则|ON|等于( )