题目内容
【题目】某家具城进行促销活动，促销方案是：顾客每消费满1000元，便可以获得奖券一张，每张奖券中奖的概率为
，若中奖，则家具城返还顾客现金1000元，某顾客购买一张价格为3400元的餐桌，得到3张奖券，设该顾客购买餐桌的实际支出为
（元）；
（1）求的所有可能取值；
（2）求的分布列和数学期望
；
【答案】（1）见解析；（2）见解析
【解析】
（1）3张奖券中奖的可能情况为：没中奖、中奖1次、中奖2次和中奖3次，故可求出
的所有可能取值；
（2）根据的所有可能取值，求出相应的概率，即可得到概率分布列，从而可求数学期望.
解：（1）3张奖券中奖的可能情况为：没中奖、中奖1次、中奖2次和中奖3次，
的所有可能取值为3400，2400，1400，400 ；
（2）
的分布列为
| 3400 | 2400 | 1400 | 400 |
P |
|
|
|
|
数学期望
阅读快车系列答案
【题目】随着网络时代的进步，流量成为手机的附带品，人们可以利用手机随时随地的浏览网页，聊天，看视频，因此，社会上产生了很多低头族.某研究人员对该地区18∽50岁的5000名居民在月流量的使用情况上做出调查，所得结果统计如下图所示：
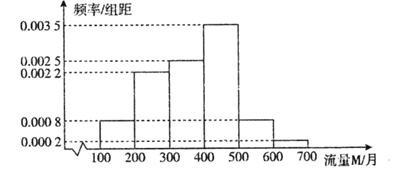
（Ⅰ)以频率估计概率，若在该地区任取3位居民，其中恰有
位居民的月流量的使用情况
在300M∽400M之间，求
的期望
；
（Ⅱ）求被抽查的居民使用流量的平均值；
（Ⅲ）经过数据分析，在一定的范围内，流量套餐的打折情况
与其日销售份数
成线性相关
关系，该研究人员将流量套餐的打折情况
与其日销售份数
的结果统计如下表所示：
折扣 | 1折 | 2折 | 3折 | 4折 | 5折 |
销售份数 | 50 | 85 | 115 | 140 | 160 |
试建立
关于
的的回归方程.
附注：回归方程
中斜率和截距的最小二乘估计公式分别为：
， 
【题目】假设关于某种设备的使用年限
(年)与所支出的维修费用
(万元)有如下统计资料：
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知
， 
.
， 
(1)求
， 
；
(2)若 与具有线性相关关系，求出线性回归方程；
(3)估计使用年限为10年时，维修费用约是多少？