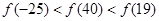题目内容
定义在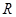 上的奇函数
上的奇函数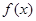 满足
满足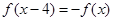 ,且在
,且在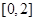 上单调递增,则
上单调递增,则
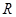 上的奇函数
上的奇函数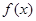 满足
满足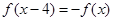 ,且在
,且在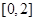 上单调递增,则
上单调递增,则A.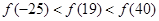 | B.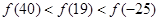 |
C.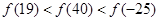 | D.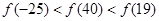 |
D
试题分析:因为
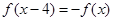 ,所以
,所以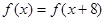 ,所以函数
,所以函数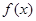 的周期是8,又可得
的周期是8,又可得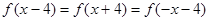 ,所以
,所以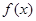 关于直线
关于直线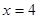 对称.所以
对称.所以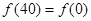 ,
,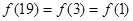 ,
,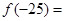
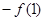 ,又
,又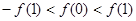 ,
,所以
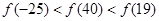
点评:本题主要考查抽象函数的基本性质,涉及到奇偶性,单调性,对称性,周期性.考查全面
具体,要求平时学习掌握知识要扎实,灵活.

练习册系列答案
相关题目
题目内容
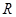 上的奇函数
上的奇函数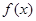 满足
满足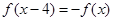 ,且在
,且在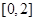 上单调递增,则
上单调递增,则A.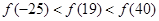 | B.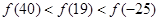 |
C.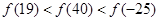 | D.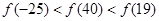 |
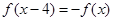 ,所以
,所以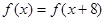 ,所以函数
,所以函数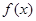 的周期是8,又可得
的周期是8,又可得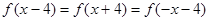 ,所以
,所以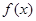 关于直线
关于直线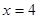 对称.所以
对称.所以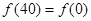 ,
,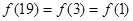 ,
,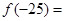
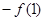 ,又
,又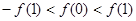 ,
,