题目内容
10.已知抛物线y2=4x,过定点A(-2,1)的直线l的斜率为k,下列情况下分别求k的取值范围:(1)l与抛物线有且仅有一个公共点;
(2)l与抛物线恰有两个公共点;
(3)l与抛物线没有公共点.
分析 由题意可得直线l的方程为y-1=k(x+2),讨论当k=0时,当k≠0时,联立抛物线方程,消去x并整理,由判别式等于0,大于0,小于0,解不等式即可得到所求范围.
解答 解:由题意可得直线l的方程为y-1=k(x+2),
当k=0时,直线l的方程为y=1,直线l与抛物线C有一个交点;
当k≠0时,直线与抛物线联立,消去x并整理,得ky2-4y+8k+4=0.
判别式△=(-4)2-4k(8k+4)=-16(k+1)(2k-1),
由△=0,得k=-1或k=$\frac{1}{2}$;由△>0,得-1$<k<\frac{1}{2}$.
所以,(1)恰好有一个公共点时,k的相应取值范围是{-1,0,$\frac{1}{2}$};
(2)恰好有两个公共点时,k的相应取值范围是{x|-1<k<$\frac{1}{2}$且k≠0};
(3)没有公共点时,k的相应取值范围是{x|x<-1,或x>$\frac{1}{2}$}.
点评 本题主要考查了由直线与抛物线的位置关系的求解参数的取值范围,考查学生的计算能力,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
18.有穷数列a1,a2,a3,…,a2015中的每一项都是-1,0,1这三个数中的某一个数,若a1+a2+a3+…+a2015=425,且(a1+1)2+(a2+1)2+(a3+1)2+…+(a2015+1)2=3870,则有穷数列a1,a2,a3,…,a2015中值为0的项数是( )
| A. | 1000 | B. | 1010 | C. | 1015 | D. | 1030 |
19.不等式4${\;}^{{x}^{2}}$<23x的解集是( )
| A. | {x|0<x<$\frac{3}{2}$} | B. | {x|0<x<3} | C. | {x|1<x<$\frac{3}{2}$} | D. | {x|$\frac{3}{2}$<x<3| |
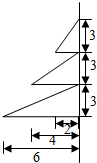 三个直角三角形如图放置,它们围绕固定直线旋转一周形成几何体,画出它的三视图,并求出它的表面积和体积.
三个直角三角形如图放置,它们围绕固定直线旋转一周形成几何体,画出它的三视图,并求出它的表面积和体积.