题目内容
15．
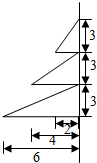三个直角三角形如图放置，它们围绕固定直线旋转一周形成几何体，画出它的三视图，并求出它的表面积和体积．
分析 由已知可得三个直角三角形围绕固定直线旋转一周形成几何体，是三个圆锥的组合体，进而可得它的三视图，及它的表面积和体积．
解答 解：由已知可得三个直角三角形围绕固定直线旋转一周形成几何体，是三个圆锥的组合体，
故该几何全的三视图如下图所示：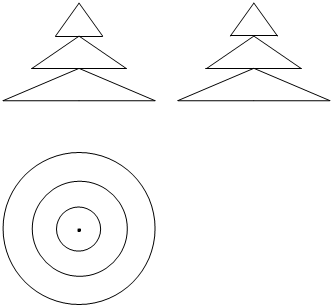
三个棱锥的底面半径分别为：2，4，6，母线长分别为：$\sqrt{13}$，5，3$\sqrt{5}$，
故棱锥的表面积S=π[2（2+$\sqrt{13}$）+4（4+5）+6（6+3$\sqrt{5}$）]=（76+2$\sqrt{13}$+18$\sqrt{5}$）π，
三个棱锥的高均为3，
故棱锥的体积V=$\frac{1}{3}$π（22+42+62）×3=56π
点评 本题考查的知识点旋转体，圆锥的表面积和体积公式，三视图，难度中档．
练习册系列答案
相关题目
20．$\sqrt{1-co{s}^{2}\frac{π}{5}}$=（ ）
| A． | sin$\frac{π}{5}$ | B． | cos$\frac{π}{5}$ | C． | -sin$\frac{π}{5}$ | D． | -cos$\frac{π}{5}$ |
