题目内容
14.(1)用二项式定理证明:32n-8n-1能被64整除(n∈N*);(2)求230-3除以7的余数.
分析 (1)把32n-8n-1=9n-8n-1利用二项式定理化为 C${\;}_{n}^{0}$8n+C${\;}_{n}^{1}$8n-1+C${\;}_{n}^{2}$8n-2+…+C${\;}_{n}^{n-2}$82,再根据每一项都是64的倍数,证得结论.
(2)把230-3利用二项式定理化为7[C${\;}_{10}^{0}$79+C${\;}_{10}^{1}$78+…+C${\;}_{10}^{9}$]-2,可得230-3除以7的余数.
解答 (1)证明:32n-8n-1=9n-8n-1=(8+1)n-8n-1=(C${\;}_{n}^{0}$8n+C${\;}_{n}^{1}$8n-1+C${\;}_{n}^{2}$8n-2+…+C${\;}_{n}^{n-2}$82+C${\;}_{n}^{n-1}$8+C${\;}_{n}^{n}$)-8n-1=C${\;}_{n}^{0}$8n+C${\;}_{n}^{1}$8n-1+C${\;}_{n}^{2}$8n-2+…+C${\;}_{n}^{n-2}$82,
由于每一项都是64的倍数,
∴32n-8n-1能被64整除.
(2)解:230-3=(23)10-3=810-3=(7+1)10-3=C${\;}_{10}^{0}$710+C${\;}_{10}^{1}$79+…+C${\;}_{10}^{9}$7+C${\;}_{10}^{10}$-3=7[C${\;}_{10}^{0}$79+C${\;}_{10}^{1}$78+…+C${\;}_{10}^{9}$]-2.
∴230-3除以7的余数为-2,即230-3除以7的余数为 5.
点评 本题主要考查二项式定理的应用,整除的基本性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
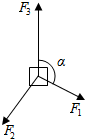 如图,一物体在水平面内的三个力F1、F2、F3的作用下保持平衡,如果F1=5N,F2=7N,∠α=120°,则F3=8N.
如图,一物体在水平面内的三个力F1、F2、F3的作用下保持平衡,如果F1=5N,F2=7N,∠α=120°,则F3=8N. 如图所示的流程图是将一系列指令和问题用框图的形式排列而成的.阅读下面的流程图,并回答下列问题.若b>c>a,则输出的数是b.
如图所示的流程图是将一系列指令和问题用框图的形式排列而成的.阅读下面的流程图,并回答下列问题.若b>c>a,则输出的数是b.