题目内容
如图,在直三棱柱ABC—A1B1C1中,AC=BC=AA1=2,∠ACB=90°,D、E、F分别为AC、AA1、AB的中点.
(Ⅰ)求EF与AC1所成角的大小;
(Ⅱ)求直线B1C1到平面DEF的距离
 .
.
(Ⅰ)求EF与AC1所成角的大小;
(Ⅱ)求直线B1C1到平面DEF的距离
 .
.解:(I)DF//BC,BC⊥AC,∴DF⊥AC…………2分
∵平面ACC1A1⊥平面ABC,∴DF⊥平面ACC1A1
∵ACC1A1是正方形 ∴AC1⊥DE…………4分
∴AC1⊥EF,即EF与AC1所成的角为90°……6分
(Ⅱ)∵B1C1∥BC,BC∥DF,∴B1C1//平面DEF…………8分
B1C1到平面DEF的距离等于点C1到平面DEF的距离
∵DF⊥平面ACC1A1 ∴平面DEF⊥平面ACC1A1
∵AC1⊥DE ∴AC1⊥平面DEF………………10分
设AC1∩DE=O,则C1O就是点C1到平面DEF的距离
由题设计算,得C1O= ………………12分
………………12分
∵平面ACC1A1⊥平面ABC,∴DF⊥平面ACC1A1
∵ACC1A1是正方形 ∴AC1⊥DE…………4分
∴AC1⊥EF,即EF与AC1所成的角为90°……6分
(Ⅱ)∵B1C1∥BC,BC∥DF,∴B1C1//平面DEF…………8分
B1C1到平面DEF的距离等于点C1到平面DEF的距离
∵DF⊥平面ACC1A1 ∴平面DEF⊥平面ACC1A1
∵AC1⊥DE ∴AC1⊥平面DEF………………10分
设AC1∩DE=O,则C1O就是点C1到平面DEF的距离
由题设计算,得C1O=
 ………………12分
………………12分略

练习册系列答案
相关题目
 是长方体
是长方体 被平面
被平面 截去几何体
截去几何体 后
后 为线段
为线段 上异于
上异于 的点,
的点, 为线段
为线段 上异于
上异于 ,则下列结论中不正确的是 ( )
,则下列结论中不正确的是 ( )

 ,且a与b不平行; ②a
,且a与b不平行; ②a 平面
平面 ,b
,b ,且
,且 ,b
,b ; ④a
; ④a 平面
平面 中,
中,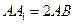 ,
, 为
为 的中点.
的中点. ∥平面
∥平面 ; (II)
; (II) 平面
平面 与平面
与平面 .
.
 是两个不同的平面,m,n是两条不同的直线,给出下列命题:
是两个不同的平面,m,n是两条不同的直线,给出下列命题: ;
; ;
;  相交;
相交;
 ,直线
,直线

 ,
,
 ,且
,且 ,则
,则 与
与 ( )
( )

 中,四边形
中,四边形 是正方形,
是正方形, 为CE上的点,且
为CE上的点,且 平面
平面 .
. 平面
平面 ;
; 的余弦值.
的余弦值.
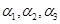 是三个相互平行的平面,平面
是三个相互平行的平面,平面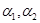 之间的距离为
之间的距离为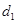 ,平面
,平面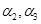 之间的距离为
之间的距离为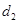 .直线
.直线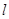 与
与 .那么
.那么 是
是 的 ( )
的 ( )
 的底面是边长为
的底面是边长为 的正方形,
的正方形, 底
底 面
面 ,
, ,点
,点 在棱
在棱 上,点
上,点 是棱
是棱 的中点
的中点 平面
平面 时,求
时,求 的长;
的长; 时,求二面角
时,求二面角 的余弦值。
的余弦值。