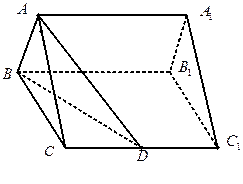题目内容
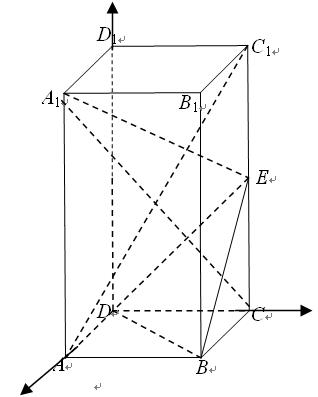
在正四棱柱 中,
中,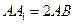 ,
, 为
为 的中点.
的中点.
求证:(I) ∥平面
∥平面 ; (II)
; (II) 平面
平面 ;
;
(自编)(Ⅲ)若E为 上的动点,试确定
上的动点,试确定 点的位置使直线
点的位置使直线 与平面
与平面 所成角的余弦值是
所成角的余弦值是 .
.

 中,
中,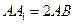 ,
, 为
为 的中点.
的中点.求证:(I)
 ∥平面
∥平面 ; (II)
; (II) 平面
平面 ;
;(自编)(Ⅲ)若E为
 上的动点,试确定
上的动点,试确定 点的位置使直线
点的位置使直线 与平面
与平面 所成角的余弦值是
所成角的余弦值是 .
.
(I)证明:连接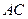 ,设
,设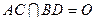 .由条件得
.由条件得
 为正方形,
为正方形,
故 为AC中点.
为AC中点.
 为
为 中点,
中点,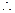
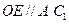 .………………2分
.………………2分
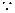
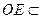 平面
平面 ,AC1(/
,AC1(/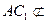 平面
平面 .
.
 ∥平面
∥平面 .………………4分
.………………4分
(II)连接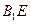 , 设
, 设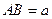 ,则在
,则在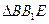 中,
中,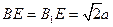 ,
,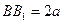 .
.
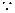
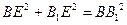 .
.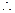 B1E^BE.
B1E^BE.
由 是正四棱柱得
是正四棱柱得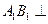 平面
平面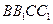 ,
,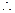
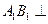
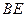 .……………6分
.……………6分
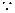
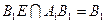
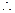
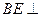 平面
平面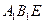 .
.
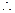
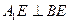 .同理
.同理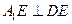 .
.
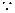
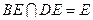
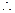
 平面
平面 .………………8分
.………………8分
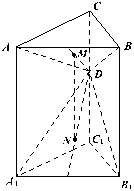
(Ⅲ)如图建立空间直角坐标系,取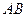 =1则
=1则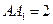
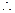
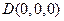 ,
,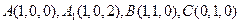 .设
.设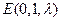
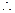
 ,
,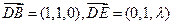 ………………9分
………………9分
设平面 的法向量
的法向量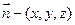
则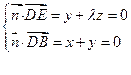 ,取
,取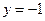 ,则
,则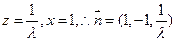 …………10分
…………10分
设直线 与平面
与平面 所成角为
所成角为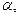 则
则
 ……11分
……11分
由题设知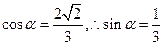 ,
,
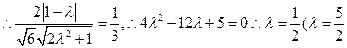 舍去)……………12分
舍去)……………12分
 为
为 靠近
靠近 的四等分点。………………13分
的四等分点。………………13分
 ,设
,设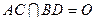 .由条件得
.由条件得 为正方形,
为正方形,故
 为AC中点.
为AC中点.
 为
为 中点,
中点,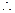
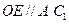 .………………2分
.………………2分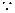
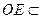 平面
平面 ,AC1(/
,AC1(/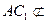 平面
平面 .
.
 ∥平面
∥平面 .………………4分
.………………4分(II)连接
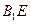 , 设
, 设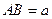 ,则在
,则在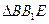 中,
中,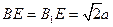 ,
,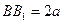 .
.
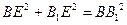 .
.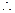 B1E^BE.
B1E^BE.由
 是正四棱柱得
是正四棱柱得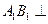 平面
平面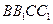 ,
,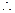
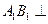
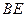 .……………6分
.……………6分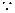
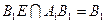
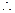
 平面
平面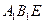 .
.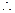
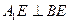 .同理
.同理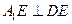 .
.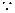
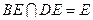
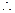
 平面
平面 .………………8分
.………………8分(Ⅲ)如图建立空间直角坐标系,取
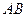 =1则
=1则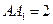

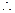
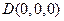 ,
,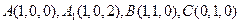 .设
.设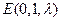
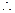
 ,
,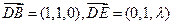 ………………9分
………………9分设平面
 的法向量
的法向量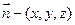
则
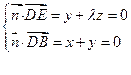 ,取
,取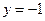 ,则
,则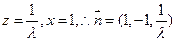 …………10分
…………10分设直线
 与平面
与平面 所成角为
所成角为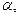 则
则 ……11分
……11分由题设知
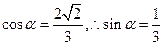 ,
,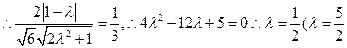 舍去)……………12分
舍去)……………12分 为
为 靠近
靠近 的四等分点。………………13分
的四等分点。………………13分略

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 α
α 平行于面
平行于面 内的无数条直线,则
内的无数条直线,则 ∥直线
∥直线 ,直线
,直线 平面
平面 中,
中,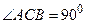 ,
, ,
, 为棱
为棱 上的一点,
上的一点, 分别为
分别为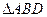 、
、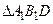 的重心.
的重心.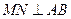 ;
; 的正切值为
的正切值为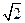 ,求两个半平面
,求两个半平面 、
、 所成锐二面角的余弦值;
所成锐二面角的余弦值; 在平面
在平面 ,试判断
,试判断 在平面
在平面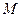 .
.
 .
. 及平面
及平面 ,则下列条件中使
,则下列条件中使 //
// 成立的是
成立的是 



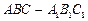 的底面正三角形的边长是2,D是
的底面正三角形的边长是2,D是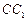 的中点,直线
的中点,直线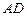 与侧面
与侧面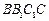 所成的角是
所成的角是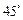 .
.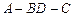 的大小;
的大小; 到平面
到平面 的距离.
的距离.