题目内容
在某两个正数x、y之间，若插入一个正数a,使x、a、y成等比数列，若另插入两个正数b、c,使x、b、c、y成等差数列.求证:(a+1)2≤(b+1)(c+1).
思路分析:本题中的两个数列是通过x、y联系在一起的，因此，我们可设法把a、b、c用x、y表示出来，以达到减元目的.
证明:由题设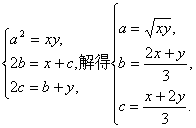
∴(b+1)(c+1)=bc+b+c+1
=
(2x+y)(x+2y)+x+y+1
=
［2(x2+y2)+5xy］+(x+y)+1
≥
(4xy+5xy)+2
+1
=(
+1)2=(a+1)2.
∴(a+1)2≤(b+1)(c+1).
练习册系列答案
全优点练单元计划系列答案
相关题目