题目内容
在某两个正数x，y之间，若插入一个数a，使x，a，y 成等差数列，若插入两个数b，c，使x，b，c，y成等比数列。
求证：（a+1）2≥（b+1）（c+1）。
求证：（a+1）2≥（b+1）（c+1）。
证明：由条件，得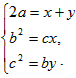
，
消去x，y，即得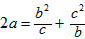
，且有a>0，b>0，c>0，
要证（a+1）2≥（b+1）（c+1），
只需证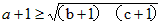
，
即证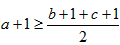
也就是证 2a≥b+c，
而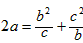
，只要证
，
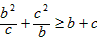即证b3+c3= （b+c）（b2+c2-bc）≥（b+c）bc，
即证b2+c2-bc≥bc，
即证（b -c）2≥0，
因为上式显然成立，
所以（a+1）2≥（b+1）（c+1）。
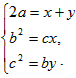，消去x，y，即得
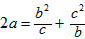，且有a>0，b>0，c>0，要证（a+1）2≥（b+1）（c+1），
只需证
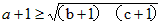，即证
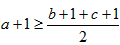
也就是证 2a≥b+c，
而
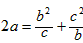，只要证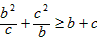，即证b3+c3= （b+c）（b2+c2-bc）≥（b+c）bc，
即证b2+c2-bc≥bc，
即证（b -c）2≥0，
因为上式显然成立，
所以（a+1）2≥（b+1）（c+1）。
练习册系列答案
相关题目