题目内容
在某两个正数x,y之间,若插入一个正数a,使x,a,y成等比数列;若插入两个正数b,c,使x,b,c,y成等差数列,求证:(a+1)2≤(b+1)(c+1).
【答案】分析:根据某两个正数x,y之间,若插入一个正数a,使x,a,y成等比数列,得到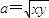 ,在根据插入两个正数b,c,使x,b,c,y成等差数列,得到b=
,在根据插入两个正数b,c,使x,b,c,y成等差数列,得到b=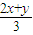 ,c=
,c=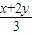 ,从而将原不等式转化为关于x,y的关系式,再利用基本不等式即可
,从而将原不等式转化为关于x,y的关系式,再利用基本不等式即可
解答:解:∵x,a,y成等比数列
∴a2=xy
∵a>1
∴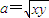
∵x,b,c,y成等差数列
∴b-x=c-b=y-c
即b=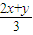 ,c=
,c=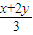
∴(b+1)(c+1)=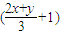 (
(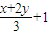 )=
)=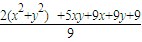
∵x>0,y>0
∴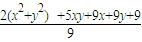 ≥
≥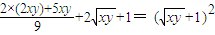 =(a+1)2
=(a+1)2
即:(a+1)2≤(b+1)(c+1).
点评:本题考查了基本不等式,等差数列与等比数列的综合,属于基础题.
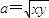 ,在根据插入两个正数b,c,使x,b,c,y成等差数列,得到b=
,在根据插入两个正数b,c,使x,b,c,y成等差数列,得到b=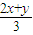 ,c=
,c=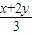 ,从而将原不等式转化为关于x,y的关系式,再利用基本不等式即可
,从而将原不等式转化为关于x,y的关系式,再利用基本不等式即可解答:解:∵x,a,y成等比数列
∴a2=xy
∵a>1
∴
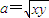
∵x,b,c,y成等差数列
∴b-x=c-b=y-c
即b=
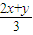 ,c=
,c=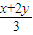
∴(b+1)(c+1)=
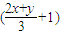 (
(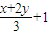 )=
)=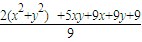
∵x>0,y>0
∴
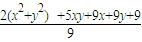 ≥
≥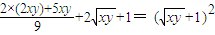 =(a+1)2
=(a+1)2即:(a+1)2≤(b+1)(c+1).
点评:本题考查了基本不等式,等差数列与等比数列的综合,属于基础题.

练习册系列答案
相关题目