题目内容
【题目】已知![]() 和
和![]() 是函数
是函数![]() 的两个零点,
的两个零点,
(1)求实数![]() 的值;
的值;
(2)设![]()
①若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
②若![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)代入函数关系式,解方程可得实数![]() 的值;(2)①恒成立问题一般利用参变分离法转化为对应函数最值问题,再根据二次函数最值求法求得对应函数最小值,即得实数
的值;(2)①恒成立问题一般利用参变分离法转化为对应函数最值问题,再根据二次函数最值求法求得对应函数最小值,即得实数![]() 的取值范围;②化简不等式,通过换元可得关于一元二次不等式,结合二次函数图像确定满足三个解的条件,最后根据实根分布列不等式组,解不等式可得实数
的取值范围;②化简不等式,通过换元可得关于一元二次不等式,结合二次函数图像确定满足三个解的条件,最后根据实根分布列不等式组,解不等式可得实数![]() 的取值范围.
的取值范围.
试题解析:(1),由已知![]() ,
, ![]()
![]()
(2)由已知可得![]() ,
,
所以![]() 在
在![]() 上恒成立可化为
上恒成立可化为![]() ,
,
化为![]() ,令
,令![]() ,则
,则![]() ,
,
因![]() ,故
,故![]() ,
,
记![]()
![]() ,因为
,因为![]() ,故
,故![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() .
.
原方程可化为![]() ,
,
令![]() 则
则![]()
![]() 有两个不等实根
有两个不等实根![]() 且
且![]() 或
或![]()
记![]()
![]() 则
则
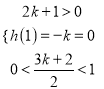 或
或![]()
两不等式组解集分别为![]() 与
与![]()
![]() 的取值范围是
的取值范围是![]()

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】某工厂36名工人的年龄数据如下表.
工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 |
1 40 | 10 36 | 19 27 | 28 34 |
2 44 | 11 31 | 20 43 | 29 39 |
3 40 | 12 38 | 21 41 | 30 43 |
4 41 | 13 39 | 22 37 | 31 38 |
5 33 | 14 43 | 23 34 | 32 42 |
6 40 | 15 45 | 24 42 | 33 53 |
7 45 | 16 39 | 25 37 | 34 37 |
8 42 | 17 38 | 26 44 | 35 49 |
9 43 | 18 36 | 27 42 | 36 39 |
(1)用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
(2)计算(1)中样本的均值x和方差s2;
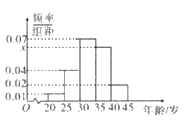
(3)36名工人中年龄在![]() 与
与![]() 之间有多少人?所占的百分比是多少(精确到0.01%)?
之间有多少人?所占的百分比是多少(精确到0.01%)?