题目内容
在正方体ABCD-A1B1C1D1中，已知E是棱C1D1的中点，则异面直线B1D1与CE所成角的余弦值的大小是
- A.
- B.
- C.
- D.
D
分析：根据题意知EF∥B1D1，所以异面直线B1D1与CE所成角与∠CEF相等或者互补，进而利用解三角形的有关知识即可求得结果．
解答：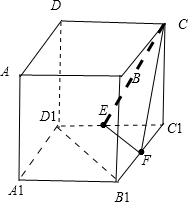
解：取C1B1的中点为F，连接EF，C1C，
因为点E、F分别为C1D1与B1C1的中点，
所以EF∥B1D1，
所以异面直线B1D1与CE所成角与∠CEF相等或者互补．
设正方体ABCD-A1B1C1D1，的棱长为2，
所以在△CEF中，EF=
，CF=CE=
，
根据余弦定理可得：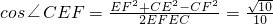
．
故选D．
点评：此题是个基础题．考查异面直线所成角问题，求解方法一般是平移法，转化为平面角问题来解决，体现了数形结合和转化的思想．
分析：根据题意知EF∥B1D1，所以异面直线B1D1与CE所成角与∠CEF相等或者互补，进而利用解三角形的有关知识即可求得结果．
解答：
解：取C1B1的中点为F，连接EF，C1C，因为点E、F分别为C1D1与B1C1的中点，
所以EF∥B1D1，
所以异面直线B1D1与CE所成角与∠CEF相等或者互补．
设正方体ABCD-A1B1C1D1，的棱长为2，
所以在△CEF中，EF=
，CF=CE=，根据余弦定理可得：
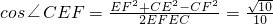．故选D．
点评：此题是个基础题．考查异面直线所成角问题，求解方法一般是平移法，转化为平面角问题来解决，体现了数形结合和转化的思想．
练习册系列答案
名校课堂系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）