题目内容
函数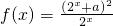 是偶函数,则a的值为
是偶函数,则a的值为
- A.0
- B.1
- C.1或-1
- D.

C
分析:若偶函数f(x)的定义域为I,则?x∈I,都有f(-x)=f(x).根据f(-x)=f(x)恒成立解决本题.
解答:因为函数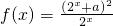 是偶函数,
是偶函数,
所以?x∈R,都有f(-x)=f(x).
所以?x∈R,都有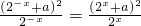
不妨取x=1,则4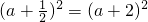 ,即a2=1
,即a2=1
解得a=-1,或a=1.
当a=1时,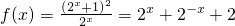 ,
,
当a=-1时,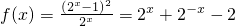 显然都为偶函数.
显然都为偶函数.
故选C.
点评:本题考查函数奇偶性,特殊值法是解决问题最便捷的方法,属基础题.
分析:若偶函数f(x)的定义域为I,则?x∈I,都有f(-x)=f(x).根据f(-x)=f(x)恒成立解决本题.
解答:因为函数
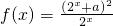 是偶函数,
是偶函数,所以?x∈R,都有f(-x)=f(x).
所以?x∈R,都有
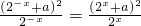
不妨取x=1,则4
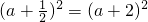 ,即a2=1
,即a2=1解得a=-1,或a=1.
当a=1时,
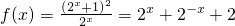 ,
,当a=-1时,
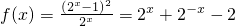 显然都为偶函数.
显然都为偶函数.故选C.
点评:本题考查函数奇偶性,特殊值法是解决问题最便捷的方法,属基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
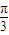 个单位长度后得到的图象对应的函数是偶函数,则a的值为 .
个单位长度后得到的图象对应的函数是偶函数,则a的值为 .