题目内容
(本小题满分12分)已知
 ,
,
 ,设函数
,设函数

 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)求函数 的单调递增区间.
的单调递增区间.

 ,
,
 ,设函数
,设函数

 .
.(Ⅰ)求函数
 的最小正周期;
的最小正周期;(Ⅱ)求函数
 的单调递增区间.
的单调递增区间.(Ⅰ)函数 的最小正周期
的最小正周期 ;
;
(Ⅱ)单调递增区间为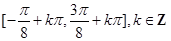 .
.
 的最小正周期
的最小正周期 ;
; (Ⅱ)单调递增区间为
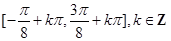 .
. 先根据数量积的坐标表示及三角恒等变换公式可求出
 ,易确定其周期,及单调递增区间.
,易确定其周期,及单调递增区间.
解:(Ⅰ)



 =
= , 5分
, 5分
∴函数 的最小正周期
的最小正周期 7分
7分
(Ⅱ)由 9分
9分
得
所以函数 在
在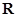 上的单调递增区间为
上的单调递增区间为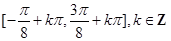 . 12分
. 12分

 ,易确定其周期,及单调递增区间.
,易确定其周期,及单调递增区间.解:(Ⅰ)




 =
= , 5分
, 5分∴函数
 的最小正周期
的最小正周期 7分
7分 (Ⅱ)由
 9分
9分得

所以函数
 在
在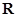 上的单调递增区间为
上的单调递增区间为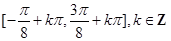 . 12分
. 12分 
练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 在同一周期内有最高点
在同一周期内有最高点 和最低点
和最低点 ,(1)求此函数
,(1)求此函数 的解析式;(2)函数
的解析式;(2)函数 的图像如何由函数
的图像如何由函数 的图像变换得到?
的图像变换得到? .
.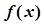 的单调递增区间;
的单调递增区间;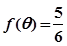 ,
,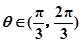 ,求
,求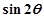 的值;
的值;  ,
, ,且
,且 .
. 的最小正周期及单调增区间;
的最小正周期及单调增区间; ,求函数
,求函数 ,其中
,其中 .设函数
.设函数 .
. 的解析式;
的解析式; ,求
,求 的值.
的值. +2m-1
+2m-1  .
. 的单调递增区间.
的单调递增区间. 函数
函数
 的图像,可将
的图像,可将 的图像( )
的图像( ) 单位,再横向压缩到原
单位,再横向压缩到原
 倍
倍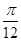 单位,再横向压缩到原
单位,再横向压缩到原 的图象如图2所示,则
的图象如图2所示,则 。
。
 ,
,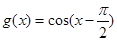 ,则下列命题中正确的是 ( )
,则下列命题中正确的是 ( ) 是偶函数
是偶函数 

