题目内容
已知向量 ,其中
,其中 .设函数
.设函数 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若 的最小值是
的最小值是 ,求
,求 的值.
的值.
 ,其中
,其中 .设函数
.设函数 .
.(Ⅰ)求
 的解析式;
的解析式;(Ⅱ)若
 的最小值是
的最小值是 ,求
,求 的值.
的值.(Ⅰ) 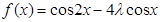 ,
,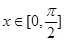 (Ⅱ)
(Ⅱ)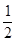
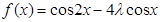 ,
,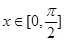 (Ⅱ)
(Ⅱ)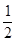
(I)利用向量数量积的坐标表示,可求出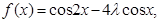
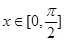 .
.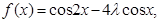
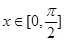
(II) ∵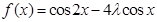
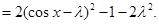
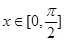 ,
,
然后可以令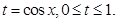 换元转化为二次函数最值来解决.
换元转化为二次函数最值来解决.
∵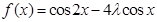
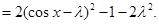
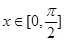
∵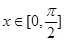 , ∴
, ∴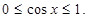
设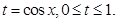
则
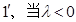 时,当且仅当
时,当且仅当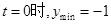 ,这与已知矛盾.
,这与已知矛盾.
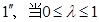 时,当且仅当
时,当且仅当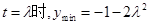 .
.
由已知得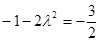 ,解得
,解得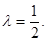
 时,当且仅当
时,当且仅当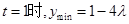 .
.
由已知得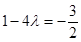 ,解得
,解得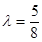 ,这与
,这与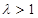 相矛盾.
相矛盾.
综上所述,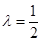 为所求.
为所求.
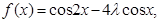
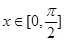 .
.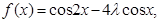
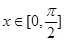
(II) ∵
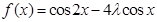
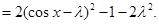
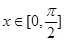 ,
,然后可以令
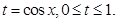 换元转化为二次函数最值来解决.
换元转化为二次函数最值来解决.∵
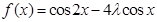
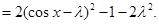
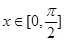
∵
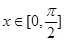 , ∴
, ∴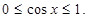
设
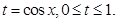
则

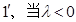 时,当且仅当
时,当且仅当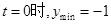 ,这与已知矛盾.
,这与已知矛盾.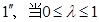 时,当且仅当
时,当且仅当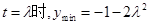 .
. 由已知得
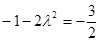 ,解得
,解得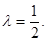
 时,当且仅当
时,当且仅当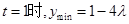 .
.由已知得
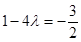 ,解得
,解得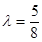 ,这与
,这与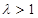 相矛盾.
相矛盾.综上所述,
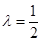 为所求.
为所求.
练习册系列答案
相关题目
 的图像按向量
的图像按向量 平移后所得函数图像的解析式为( ).
平移后所得函数图像的解析式为( ).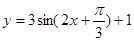



 ,
,
 ,设函数
,设函数 .
. 的值域;
的值域; 的三个内角分别为
的三个内角分别为 ,
, ,
, ,若
,若 ,
, ,求
,求 的值.
的值. (其中
(其中 ,
, ,
,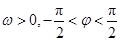 )的部分图象如图所示.
)的部分图象如图所示.
 ,
, ,
, 的值;
的值; 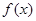 图象上的三点
图象上的三点 的横坐标分别为
的横坐标分别为 ,求
,求 的值.
的值.
 ,
,
 ,设函数
,设函数
 .
. 的最小正周期;
的最小正周期; 的周期为
的周期为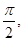
 的单调递增区间;
的单调递增区间; 、
、 、
、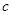 满足
满足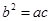 ,且边
,且边 ,求此时函数
,求此时函数 和函数
和函数 在
在 内都是
内都是 的图象如图所示,则
的图象如图所示,则 和
和 的取值是( )
的取值是( )




 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的图象,则
的图象,则