题目内容
1.已知a,b,x,y∈(0,+∞),(Ⅰ)求证:$\frac{{a}^{2}}{x}$+$\frac{{b}^{2}}{y}$≥$\frac{(a+b)^{2}}{x+y}$,并指出等号成立的条件;
(Ⅱ)利用(1)中的不等式求函数f(x)=$\frac{2}{x}$+$\frac{9}{1-2x}$(x∈(0,$\frac{1}{2}$))的最小值,并求出等号成立时的x值(必须使用(1)中的结论,否则不给分).
分析 (Ⅰ)判断$\frac{{a}^{2}}{x}$+$\frac{{b}^{2}}{y}$-$\frac{(a+b)^{2}}{x+y}$的符号,得到大小关系;
(Ⅱ)对f(x)变形,利用基本你打算求之.
解答 解:(Ⅰ)$\frac{{a}^{2}}{x}$+$\frac{{b}^{2}}{y}$-$\frac{(a+b)^{2}}{x+y}$=$\frac{(ay-bx)^{2}}{xy(x+y)}$…(3分)
∵a,b,x,y∈(0,+∞),
∴xy(x+y)>0,(ay-bx)2≥0
所以$\frac{{a}^{2}}{x}$+$\frac{{b}^{2}}{y}$≥$\frac{(a+b)^{2}}{x+y}$,…(5分)
等号当且仅当ay=bx时成立.…(6分)
(Ⅱ)f(x)=$\frac{2}{x}$+$\frac{9}{1-2x}$=$\frac{4}{2x}+\frac{9}{1-2x}≥\frac{(2+3)^{2}}{2x+1-2x}$=25,…(10分)
等号当且仅当2(1-2x)=3×2x即x=$\frac{1}{5}$∈(0,$\frac{1}{2}$)时成立,…(11分)
所以,x=$\frac{1}{5}$时,f(x)的最小值为25.…(12分)
点评 本题考查了比较法证明不等式、利用基本不等式求最值.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
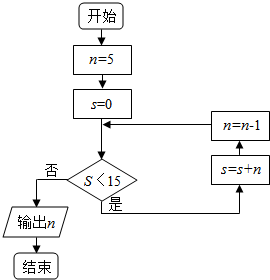
12.如图所示,程序执行后的输出结果为( )

| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
16.用数学归纳法证明对任意正整数n,都有$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$>$\frac{13}{24}$的过程中,由n=k推导n=k+1时,不等式的左边增加的式子为( )
| A. | $\frac{1}{2k+2}$ | B. | $\frac{1}{2k+1}$+$\frac{1}{2k+2}$ | C. | $\frac{1}{2k+1}$-$\frac{1}{2k+2}$ | D. | $\frac{1}{2k+1}$-$\frac{3}{2k+2}$ |
13.已知实数x,y满足不等式组$\left\{{\begin{array}{l}{2x-y+2≥0}\\{x+y-2≥0}\\{x≤2}\end{array}}\right.$,则$\frac{y-1}{x+3}$的取值范围是( )
| A. | $(-∞,-\frac{1}{5}]∪[1,+∞)$ | B. | $[\frac{1}{3},1]$ | C. | [-$\frac{1}{5}$,$\frac{1}{3}$] | D. | [-$\frac{1}{5}$,1] |