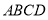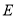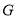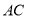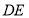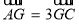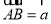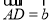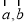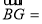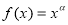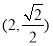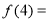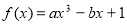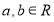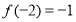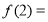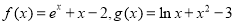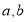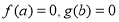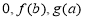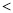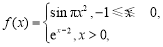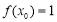题目内容
设函数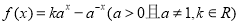 ,
, 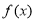 是定义域为
是定义域为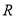 的奇函数.
的奇函数.
(Ⅰ)求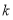 的值,判断并证明当
的值,判断并证明当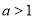 时,函数
时,函数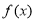 在
在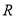 上的单调性;
上的单调性;
(Ⅱ)已知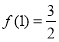 ,函数
,函数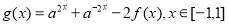 ,求
,求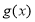 的值域;
的值域;
(Ⅲ)已知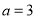 ,若
,若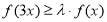 对于
对于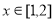 时恒成立.请求出最大的整数
时恒成立.请求出最大的整数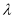 .
.
(Ⅰ)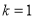 ,
,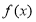 在R上为增函数;(Ⅱ)
在R上为增函数;(Ⅱ)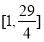 ;(Ⅲ)
;(Ⅲ)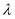 的最大整数为10.
的最大整数为10.
【解析】
试题分析:(Ⅰ)由奇函数的性质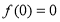 得
得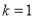 ,由单调性的定义证明
,由单调性的定义证明 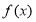 在R上是增函数;
在R上是增函数;
(Ⅱ)由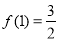 可得
可得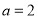 ,
,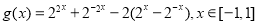 ,由换元法令
,由换元法令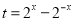 ,将函数转化为二次函数
,将函数转化为二次函数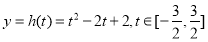 求最值;(Ⅲ)
求最值;(Ⅲ)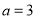 时,原式可化为
时,原式可化为 ,令
,令 ,由分离参数的方法得到
,由分离参数的方法得到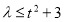 ,进而得到
,进而得到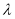 的取值范围.本题中用到换元法,换元之后应特别注意变元
的取值范围.本题中用到换元法,换元之后应特别注意变元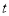 的取值范围.
的取值范围.
试题解析:(Ⅰ)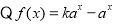 是定义域为R上的奇函数,
是定义域为R上的奇函数, 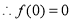 ,得
,得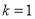 .
.
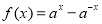 ,
,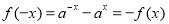 ,即
,即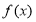 是R上的奇函数 2分
是R上的奇函数 2分
设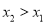 ,则
,则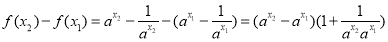 ,
,
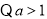 ,
,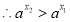 ,
,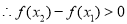 ,
, 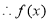 在R上为增函数 5分
在R上为增函数 5分
(Ⅱ)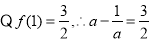 ,即
,即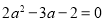 ,
,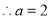 或
或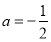 (舍去)
(舍去)
则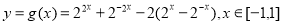 ,令
,令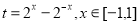 ,
,
由(1)可知该函数在区间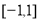 上为增函数,则
上为增函数,则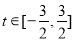
则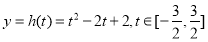 8分
8分
当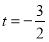 时,
时,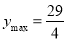 ;当
;当 时,
时,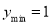
所以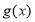 的值域为
的值域为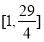 10分
10分
(Ⅲ)由题意,即 ,在
,在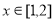 时恒成立
时恒成立
令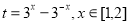 ,则
,则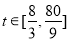
则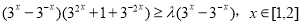 恒成立
恒成立
即为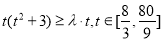 恒成立 13分
恒成立 13分
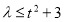 ,
,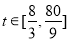 恒成立,当
恒成立,当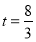 时,
时,
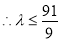 ,则
,则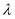 的最大整数为10 16分
的最大整数为10 16分
考点:函数的奇偶性,单调性,换元法求函数的最值,用分离参数的方法求参数的取值范围.

练习册系列答案
相关题目