题目内容
已知 ( )
( )
A.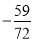 B.
B.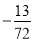 C.
C. D.
D.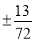
A
【解析】
试题分析:由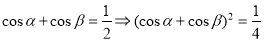 即
即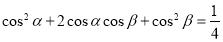 ①
①
由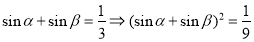 即
即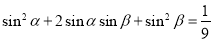 ②
②
所以①+②可得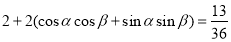 即
即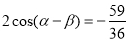 即
即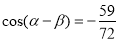 ,选A.
,选A.
考点:1.同角三角函数的基本关系式;2.两角差的余弦公式.

练习册系列答案
相关题目
题目内容
已知 ( )
( )
A.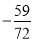 B.
B.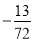 C.
C. D.
D.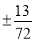
A
【解析】
试题分析:由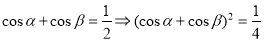 即
即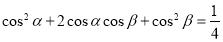 ①
①
由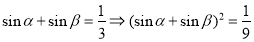 即
即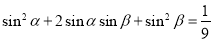 ②
②
所以①+②可得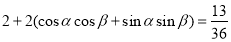 即
即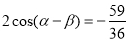 即
即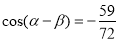 ,选A.
,选A.
考点:1.同角三角函数的基本关系式;2.两角差的余弦公式.
