题目内容
设a为实数,函数f(x)=x3+ax2+(a-3)x的导函数为 ,且
,且 是偶函数, 则曲线:y=f(x)在点(2,f(2))处的切线方程为 .
是偶函数, 则曲线:y=f(x)在点(2,f(2))处的切线方程为 .
 ,且
,且 是偶函数, 则曲线:y=f(x)在点(2,f(2))处的切线方程为 .
是偶函数, 则曲线:y=f(x)在点(2,f(2))处的切线方程为 . 9x—y—16 = 0
试题分析:
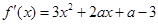 ,因为
,因为 是偶函数,所以
是偶函数,所以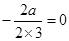 ,解得a=0,所以
,解得a=0,所以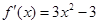
切线的斜率k=
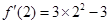 =9,f(2)=23-3×2=2,所求切线方程为y-2=9(x-2),即9x—y—16 = 0.
=9,f(2)=23-3×2=2,所求切线方程为y-2=9(x-2),即9x—y—16 = 0.
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
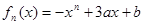 (
(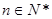 ,
,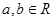 )。
)。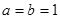 ,求
,求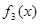 在
在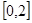 上的最大值和最小值;
上的最大值和最小值;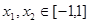 ,都有
,都有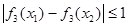 ,求
,求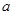 的取值范围;
的取值范围;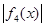 在
在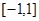 上的最大值为
上的最大值为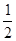 ,求
,求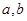 的值。
的值。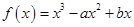 的图象与直线
的图象与直线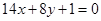 相切于点
相切于点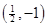 .
.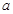 和
和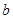 的值; (2)求
的值; (2)求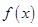 的极值.
的极值.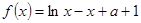
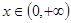 使得
使得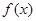 ≥0成立,求
≥0成立,求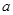 的范围
的范围 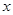 >1时,在(1)的条件下,
>1时,在(1)的条件下,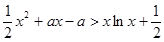 成立
成立 ,
, (
( ,
, 为自然对数的底数).
为自然对数的底数). 时,求
时,求 的单调区间;
的单调区间; ,
, 恒成立,求
恒成立,求 的最小值;
的最小值; ,在
,在 上总存在两个不同的
上总存在两个不同的 ,使得
,使得 成立,求
成立,求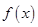 在R上可导,函数
在R上可导,函数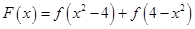 ,则
,则 .
. 的图象在点
的图象在点 处的切线方程为
处的切线方程为 ,则函数
,则函数 的图象在点
的图象在点 处的切线方程为 .
处的切线方程为 .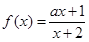 在
在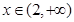 上单调递减,则实数
上单调递减,则实数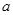 的取值范围是 .
的取值范围是 .