题目内容
设函数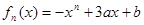 (
(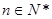 ,
,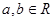 )。
)。
⑴若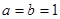 ,求
,求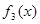 在
在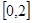 上的最大值和最小值;
上的最大值和最小值;
⑵若对任意 ,都有
,都有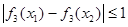 ,求
,求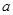 的取值范围;
的取值范围;
⑶若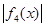 在
在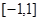 上的最大值为
上的最大值为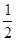 ,求
,求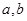 的值。
的值。
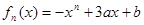 (
(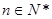 ,
,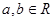 )。
)。⑴若
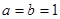 ,求
,求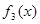 在
在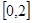 上的最大值和最小值;
上的最大值和最小值;⑵若对任意
 ,都有
,都有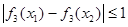 ,求
,求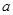 的取值范围;
的取值范围;⑶若
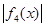 在
在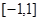 上的最大值为
上的最大值为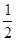 ,求
,求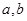 的值。
的值。(1)最大值为3,最小值为-1;(2)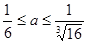 ;(3)
;(3)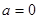 ,
,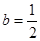 .
.
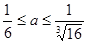 ;(3)
;(3)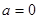 ,
,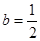 .
.试题分析:(1)
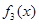 是三次函数,要求它的最大值和最小值一般利用导数来求,具体的就是令
是三次函数,要求它的最大值和最小值一般利用导数来求,具体的就是令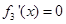 ,求出
,求出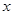 ,再讨论相应区间的单调性,就可判断出函数什么时候取最大值,什么时候取最小值;(2)要求
,再讨论相应区间的单调性,就可判断出函数什么时候取最大值,什么时候取最小值;(2)要求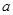 的取值范围,题中没有其他的信息,因此我们首先判断出
的取值范围,题中没有其他的信息,因此我们首先判断出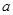 的初始范围,由已知有
的初始范围,由已知有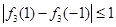 ,得出
,得出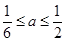 ,而此时
,而此时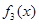 在
在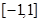 上的单调性不确定,通过讨论单调性,求出
上的单调性不确定,通过讨论单调性,求出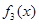 在
在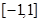 上的最大值和最小值,为什么要求最大值
上的最大值和最小值,为什么要求最大值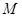 和最小值
和最小值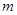 呢?原因就在于题设条件等价于最大值与最小值的差
呢?原因就在于题设条件等价于最大值与最小值的差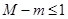 ,这样就有求出
,这样就有求出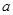 的取值范围了;(3)对
的取值范围了;(3)对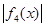 在
在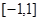 上的最大值为
上的最大值为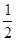 的处理方法,同样我们用特殊值法,首先
的处理方法,同样我们用特殊值法,首先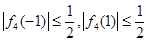 ,即
,即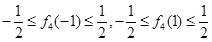 ,由这两式可得
,由这两式可得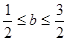 ,而特殊值
,而特殊值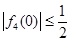 ,又能得到
,又能得到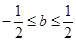 ,那么只能有
,那么只能有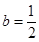 ,把
,把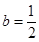 代入
代入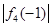 和
和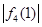 ,就可求出
,就可求出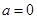 .
.试题解析:(1)
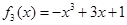 ,∴
,∴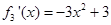 , 2分
, 2分∴在
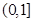 内,
内,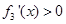 ,在
,在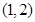 内,
内,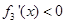 ,
,∴在
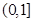 内,
内,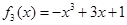 为增函数,在
为增函数,在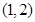 内,
内,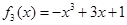 为减函数,
为减函数,∴
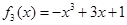 的最大值为
的最大值为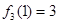 ,最小值为
,最小值为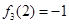 , 4分
, 4分(2)∵对任意
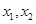 有
有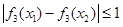 ,∴
,∴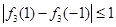 ,
,从而有
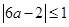 ,∴
,∴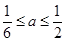 . 6分
. 6分又
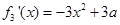 ,∴
,∴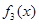 在
在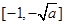 ,
,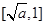 内为减函数,在
内为减函数,在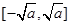 内为增函数,只需
内为增函数,只需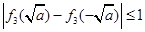 ,则
,则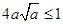 ,
,∴
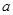 的取值范围是
的取值范围是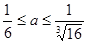 10分[
10分[(3)由
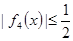 知
知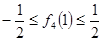 ①
①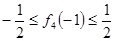 ②,
②,①加②得
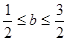 又∵
又∵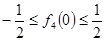 ∴
∴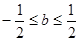 ∴
∴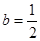 14分
14分将
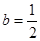 代入①②得
代入①②得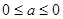 ∴
∴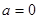 16分
16分
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
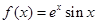 函数.
函数.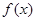 单调递增区间;
单调递增区间;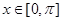 时,求函数
时,求函数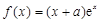 ,其中
,其中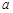 为常数.
为常数. 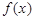 是区间
是区间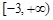 上的增函数,求实数
上的增函数,求实数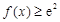 在
在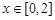 时恒成立,求实数
时恒成立,求实数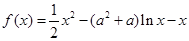 .
.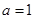 ,求曲线
,求曲线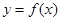 在点
在点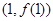 处的切线方程;
处的切线方程;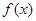 的单调性.
的单调性.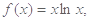
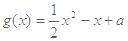 .
.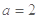 时,求
时,求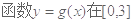 上的值域;
上的值域;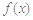 在
在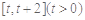 上的最小值;
上的最小值;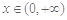 ,都有
,都有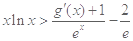 成立
成立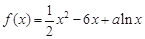 的一个极值点。
的一个极值点。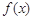 在区间
在区间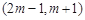 上单调递减,求实数m的取值范围;
上单调递减,求实数m的取值范围;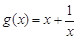 ,对于任意
,对于任意 和
和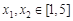 ,有不等式
,有不等式 恒成立,求实数
恒成立,求实数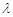 的取值范围.
的取值范围.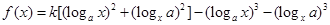 ,
,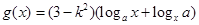 ,(其中
,(其中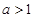 ),设
),设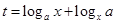 .
.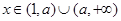 时,试将
时,试将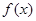 表示成
表示成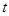 的函数
的函数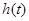 ,并探究函数
,并探究函数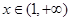 时,若存在
时,若存在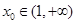 ,使
,使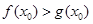 成立,试求
成立,试求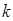 的范围.
的范围.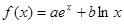 (
(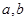 为常实数)的定义域为
为常实数)的定义域为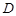 ,关于函数
,关于函数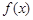 给出下列命题:
给出下列命题: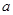 ,存在正数
,存在正数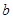 ,使得对于任意的
,使得对于任意的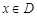 ,都有
,都有 .
.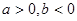 时,函数
时,函数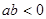 时,则
时,则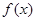 一定存在极值点;
一定存在极值点; 时,方程
时,方程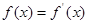 在区间(1,2)内有唯一解.
在区间(1,2)内有唯一解.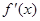 ,且
,且