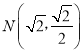题目内容
【题目】设圆C与两圆![]() ,
,![]() 中的一个内切,另一个外切.
中的一个内切,另一个外切.
(1)求C的圆心轨迹L的方程;
(2)已知点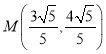 ,
,![]() ,且P为L上动点,求
,且P为L上动点,求![]() 的最大值及此时点P的坐标.
的最大值及此时点P的坐标.
【答案】(1)![]() ;(2)
;(2)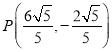 ;最大值2.
;最大值2.
【解析】
(1)设出圆心坐标,根据相切关系建立等式,结合双曲线的定义可求轨迹方程;
(2)求出直线![]() 的方程,联立双曲线方程求出交点坐标,结合几何性质可求结果.
的方程,联立双曲线方程求出交点坐标,结合几何性质可求结果.
(1)设圆C的圆心坐标为![]() ,
,![]() ,由题意,
,由题意,
![]() 或
或![]() ,
,
所以![]()
所以圆心![]() 的轨迹是以原点为中心,焦点在
的轨迹是以原点为中心,焦点在![]() 轴上, 且实轴为4,焦距为
轴上, 且实轴为4,焦距为![]() 的双曲线,
的双曲线,
![]() ,
,
故![]() 的圆心轨迹
的圆心轨迹![]() 的方程为
的方程为![]() .
.
(2)过点![]() 的直线
的直线![]() 方程为
方程为![]() ,代入
,代入![]() ,
,
解得![]() .
.
故直线![]() 与
与![]() 的交点为
的交点为 .
.
因为![]() 在线段
在线段![]() 外,
外,![]() 在线段
在线段![]() 上,故
上,故![]() ,
,
![]() .
.
若点![]() 不在
不在![]() 上,则
上,则![]() , 若点
, 若点![]() 在
在![]() 处,则
处,则![]() ;
;
综上所述,![]() 只在点
只在点![]() 处取到最大值2,此时点
处取到最大值2,此时点![]() 的坐标为
的坐标为
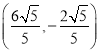 .
.

练习册系列答案
相关题目