题目内容
正四棱锥P-ABCD的高为PO,若Q为CD中点,且
=
+x
+y
(x,y∈R)则x+y=
| OQ |
| PQ |
| PC |
| PA |
-1
-1
.分析:由题设条件,作出图形,结合图形知:
=
+
=
+
+
=
+
-
=
-
-
,所以x=y=-
,由此能求出结果.
| OQ |
| PQ |
| OP |
| PQ |
| OA |
| AP |
| PQ |
| 1 |
| 2 |
| CA |
| PA |
| PQ |
| 1 |
| 2 |
| PA |
| 1 |
| 2 |
| PC |
| 1 |
| 2 |
解答: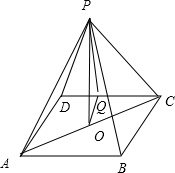 解:如图,正四棱锥P-ABCD的高为PO,若Q为CD中点,
解:如图,正四棱锥P-ABCD的高为PO,若Q为CD中点,
=
+
=
+
+
=
+
-
=
+
(
-
)-
=
-
-
,
∵
=
+x
+y
(x,y∈R)
∴x=y=-
,
∴x+y=-1.
故答案为:-1.
 解:如图,正四棱锥P-ABCD的高为PO,若Q为CD中点,
解:如图,正四棱锥P-ABCD的高为PO,若Q为CD中点,| OQ |
| PQ |
| OP |
=
| PQ |
| OA |
| AP |
=
| PQ |
| 1 |
| 2 |
| CA |
| PA |
=
| PQ |
| 1 |
| 2 |
| PA |
| PC |
| PA |
=
| PQ |
| 1 |
| 2 |
| PA |
| 1 |
| 2 |
| PC |
∵
| OQ |
| PQ |
| PC |
| PA |
∴x=y=-
| 1 |
| 2 |
∴x+y=-1.
故答案为:-1.
点评:本题考查空间向量的基本定理及其意义,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
相关题目
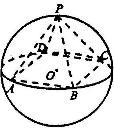 如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,如果VP-ABCD=
如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,如果VP-ABCD=| 16 |
| 3 |
| A、4π | B、8π |
| C、12π | D、16π |
 (2009•温州一模)如图是正四棱锥P-ABCD的三视图,其中正视图是边长为1的正三角形,则这个四棱锥的表面积是( )
(2009•温州一模)如图是正四棱锥P-ABCD的三视图,其中正视图是边长为1的正三角形,则这个四棱锥的表面积是( )