题目内容
正四棱锥P-ABCD的侧棱和底面边长都等于2
,则它的外接球的表面积是( )
| 2 |
分析:先画出图形,正四棱锥外接球的球心在它的底面的中心,然后根据勾股定理解出球的半径,最后根据球的表面积公式即可求解.
解答:解:如图,设正四棱锥底面的中心为O1,设外接球的球心为O,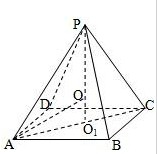
则O在正三棱锥的高PO上.
在直角三角形ABC中,AC=
AB=
×2
=4,
AO1=2,则高PO1=
=
=
=
=2,
则OO1=PO1-R=2-R,OA=R,
在直角三角形AO1O中,R2=(2-R)2+22,
解得R=2.
即正四棱锥外接球的球心在它的底面的中心O1O,且球半径R=2,
球的表面积S=4πr2=16π
故选A.

则O在正三棱锥的高PO上.
在直角三角形ABC中,AC=
| 2 |
| 2 |
| 2 |
AO1=2,则高PO1=
AP2-A
|
(2
|
| 8-4 |
| 4 |
则OO1=PO1-R=2-R,OA=R,
在直角三角形AO1O中,R2=(2-R)2+22,
解得R=2.
即正四棱锥外接球的球心在它的底面的中心O1O,且球半径R=2,
球的表面积S=4πr2=16π
故选A.
点评:本题主要考查球的表面积,考查计算能力和空间想象能力,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
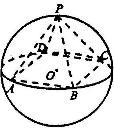 如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,如果VP-ABCD=
如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,如果VP-ABCD=| 16 |
| 3 |
| A、4π | B、8π |
| C、12π | D、16π |
 (2009•温州一模)如图是正四棱锥P-ABCD的三视图,其中正视图是边长为1的正三角形,则这个四棱锥的表面积是( )
(2009•温州一模)如图是正四棱锥P-ABCD的三视图,其中正视图是边长为1的正三角形,则这个四棱锥的表面积是( )