题目内容
与向量
=（
，1），
=（1，
）的夹角相等且模为
的向量为 （ ）
A． | B． |
C． | D． |
C
解析试题分析：设所求向量的坐标为
（x，y），因为模为，所以x2+y2=4…………………①
因为与向量=（，1），=（1，）的夹角相等，所以
=
，
即
=
……………………………………………………………………②
①②联立解得：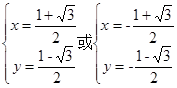
，因此答案为C。
考点：本题考查向量的数量积；数量积的坐标运算；平面向量的坐标形式。
点评：本题考查向量的数量积，利用坐标运算以及向量相等，列出方程组求出点的坐标是解题的关键，考查计算能力．
练习册系列答案
相关题目
空间直角坐标系中，O为坐标原点，已知两点坐标为A（3，1，0），B（－1，3，0），若点C满足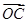
＝
＋
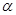
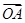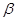
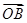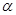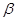，其中，∈R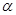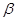，＋＝1，则点C的轨迹为
| A．平面 | B．直线 | C．圆 | D．线段 |
已知点
是
的重心，
若
，
，则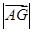
的最小值是（ ）
A． | B． | C． | D． |
O是
所在平面内一点，且满足
，则点O是的（ ）
| A．三条内角平分线交点（即内心） | B．三边的垂直平分线交 点（即外心） |
| C．三条高线的交点（即垂心） | D．三条中线交点（即重心） |
已知非零向量
与
满足（
+
）·
=0,且·=-
,则△ABC为（ ）
| A．等腰非等边三角形 | B．等边三角形 |
| C．三边均不相等的三角形 | D．直角三角形 |
，下列条件中能确定的M与点A、B、C一定共面的是（ ）
在四边形
中，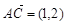
，
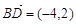,则该四边形的面积为（ ）
A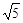． | B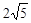． | C．5 | D．10 |
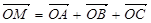
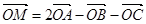
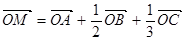
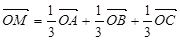
，若a=e1+3e2，b=2e1，则向量a在b方向上的射影为________.