题目内容
已知
f(x)是定义在R上的不恒为零的函数,且对于任意的a,bÎ R都满足:f(ab)=af(b)+bf(a)
(1)
求f(0),f(1)的值;(2)
判断f(x)的奇偶性,并证明你的结论.
答案:略
解析:
解析:
|
(1)f(0)=f(0 ·0)=0·f(0)+0·f(0)=0由 f(1)=f(1·1)=1·f(1)+1·f(1)得 f(1)=0(2)f(x) 是奇函数∵ 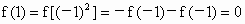
∴ f(-1)=0f( -x)=f(-1·x)=-f(x)+xf(-1)=-f(x)因此 f(x)为奇函数 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 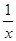 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
