题目内容
已知平行四边形ABCD的顶点A(3,-1)、C(2,-3),点D在直线3x-y+1=0上移动,则点B的轨迹方程为( )
| A.3x-y-20=0(x≠3) | B.3x-y-10=0(x≠3) |
| C.3x-y-9=0(x≠2) | D.3x-y-12=0(x≠5) |
A
试题分析:设B(x,y),D(m,n),因为ABCD是平行四边形,所以AC和BD的中点相同,即
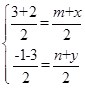 ,即
,即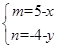 ,因为点D在直线3x-y+1=0上移动,所以3x-y-20=0,又x=2时,A、B、C三点共线,所以x≠2,所以点B的轨迹方程为3x-y-9=0(x≠2) 。
,因为点D在直线3x-y+1=0上移动,所以3x-y-20=0,又x=2时,A、B、C三点共线,所以x≠2,所以点B的轨迹方程为3x-y-9=0(x≠2) 。点评:求完轨迹方程,一定要注意验证,别产生增根,也不要漏根。此题要是填空题就非常容易出错。

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
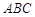 中,点
中,点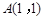 ,
,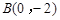 ,
,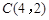 ,
,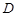 为
为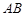 的中点,
的中点,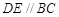 .
. 边上的高所在直线的方程;
边上的高所在直线的方程;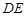 所在直线的方程.
所在直线的方程. 在
在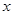 轴上的截距为
轴上的截距为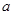 ,在
,在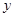 轴上的截距为
轴上的截距为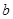 ,则( )
,则( )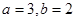
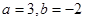
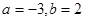
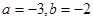
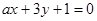 与直线
与直线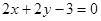 互相垂直,那么
互相垂直,那么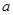 的值等于( )
的值等于( )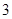
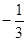
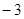
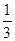
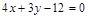 的距离为 .
的距离为 .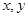 满足
满足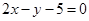 ,则
,则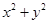 的最小值为________.
的最小值为________.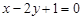 关于直线
关于直线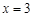 对称的直线方程为 .
对称的直线方程为 .