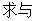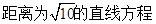题目内容
(本小题满分8分)已知直线l垂直于直线3x-4y-7=0,直线l与两坐标轴围成的三角形的周长为10,求直线l的方程
解:设直线l方程为4x+3y+b=0, ------------------1分
则l与?x轴、y轴的交点为A(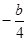 ,0),B(0,
,0),B(0, ).---------- 3分
).---------- 3分
∴|AB|=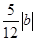 . ---------------------- 4分
. ---------------------- 4分
由|OA|+|OB|+|AB|=10,
得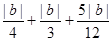 =10.∴b=±10. ------------------- 7分
=10.∴b=±10. ------------------- 7分
∴l方程为4x+3y+10=0,4x+3y-10=0. ------8分
则l与?x轴、y轴的交点为A(
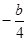 ,0),B(0,
,0),B(0, ).---------- 3分
).---------- 3分∴|AB|=
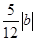 . ---------------------- 4分
. ---------------------- 4分由|OA|+|OB|+|AB|=10,
得
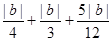 =10.∴b=±10. ------------------- 7分
=10.∴b=±10. ------------------- 7分∴l方程为4x+3y+10=0,4x+3y-10=0. ------8分
试题分析:因为直线l垂直于直线3x-4y-7=0,所以设直线l方程为4x+3y+b=0,再分别求出A,B点的坐标,利用两点间距离公式求出三角形ABO的三边长,根据三角形ABO的周长为10,就可得到参数B的值,求得直线l的方程.
点评:解决该试题的关键是利用垂直关系,设直线l方程为4x+3y+b=0,再分别求出A,B点的坐标,和三角形ABO的三边长。

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
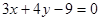 和
和 的距离是( )
的距离是( )


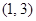 且在
且在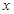 轴的截距为
轴的截距为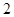 的直线方程是____________________.
的直线方程是____________________.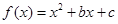 的导函数
的导函数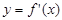 的图象如图所示,且
的图象如图所示,且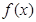 满足
满足 ,那么
,那么
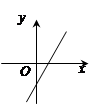

 和
和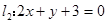 的交点
的交点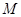 , 且射到
, 且射到 轴上一点
轴上一点 后被
后被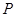 的坐标;
的坐标; 的方程.
的方程.