题目内容
如图,将圆分成n个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为an.
(1) ;
;
(2)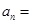 .
.
(1)18;(2)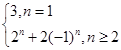 .
.
解析试题分析:(1)设三种不同颜色分别为甲、乙、丙三种. 时,第1区域有3种选择, 第2区域有2种选择,第3区域有2种选择,因为第4区域要与第1区域颜色不同,故对第3区域的选择分类讨论:当第3区域与第1区域颜色相同时,第4区域有2种选择;当第3区域与第1区域颜色不同时,第4区域仅有1种选择.所以
时,第1区域有3种选择, 第2区域有2种选择,第3区域有2种选择,因为第4区域要与第1区域颜色不同,故对第3区域的选择分类讨论:当第3区域与第1区域颜色相同时,第4区域有2种选择;当第3区域与第1区域颜色不同时,第4区域仅有1种选择.所以 ;(2)当将圆分成n个区域,用3种不同颜色给每一个区域染色时,第1区域有3种染色方案,第2区域至第
;(2)当将圆分成n个区域,用3种不同颜色给每一个区域染色时,第1区域有3种染色方案,第2区域至第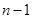 区域有2种染色方案.此时考虑第
区域有2种染色方案.此时考虑第 区域也有2种涂色方案,在此情况下有两种情况:
区域也有2种涂色方案,在此情况下有两种情况:
情况一:第 区域与第1区域同色,此时相当将这两区域重合,这时问题转化为3种不同颜色给圆上
区域与第1区域同色,此时相当将这两区域重合,这时问题转化为3种不同颜色给圆上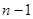 个区域涂色,即为
个区域涂色,即为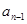 种染色方案;
种染色方案;
情况二:第 区域与第1区域不同色,此时问题就转化为用3种不同颜色给圆上
区域与第1区域不同色,此时问题就转化为用3种不同颜色给圆上 个区域染色,且相邻区域颜色互异,即此时的情况就是
个区域染色,且相邻区域颜色互异,即此时的情况就是 .根据分类原理可知
.根据分类原理可知 ,且满足初始条件:
,且满足初始条件: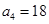 .
.
即递推公式为 ,由
,由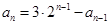 变形得
变形得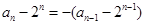 ,所以数列
,所以数列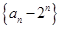 是以-1为公比的等比数列.所以
是以-1为公比的等比数列.所以 ,即
,即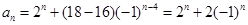 .当
.当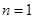 时,易知有3种染色方法,即
时,易知有3种染色方法,即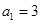 ,不满足上述通项公式;当
,不满足上述通项公式;当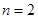 时,易知有
时,易知有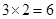 种染色方法,即
种染色方法,即 ,满足上述通项公式;当
,满足上述通项公式;当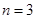 时,易知有
时,易知有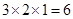 种染色方法,即
种染色方法,即 ,满足上述通项公式.
,满足上述通项公式.
综上所述, .
.
考点:数列的递推公式与通项公式、排列组合

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
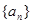 的前
的前 项和
项和 (
( ),则
),则 的值是__________.
的值是__________. 中,
中, ,则
,则 .
. 的首项
的首项 ,前n项和为Sn ,且满足
,前n项和为Sn ,且满足 ( n∈N*) .则满足
( n∈N*) .则满足 的所有n的和为 .
的所有n的和为 . 的前n项和
的前n项和 ,则
,则 的值为 .
的值为 . 行有
行有 ,每个数是它下一行左右相邻两数的和,如:
,每个数是它下一行左右相邻两数的和,如: …,则第
…,则第 行第3个数字是 .
行第3个数字是 .
 为等比数列,
为等比数列, 是它的前
是它的前 项和。若
项和。若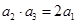 ,且
,且 与
与 的等差中项为
的等差中项为 ,则
,则 = .
= .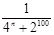 (n="1," 2, ),则S99=a1+a2+ +a99=
(n="1," 2, ),则S99=a1+a2+ +a99=