题目内容
已知f（x）=（a-2）x2+2（a-2）x-4．
（1）当a=3时，解关于x的不等式f（x）≥-1；
（2）若f（x）＜0对一切x∈R恒成立，试确定实数a的取值范围．
（1）当a=3时，解关于x的不等式f（x）≥-1；
（2）若f（x）＜0对一切x∈R恒成立，试确定实数a的取值范围．
（1）当a=3时，f（x）=x2+2x-4，
∴f（x）≥-1，即x2+2x-4≥-1，即x2+2x-3≥0，
∴x≤-3或x≥1，
∴关于x的不等式f（x）≥-1的解集为{x|x≤-3或x≥1}；
（2）f（x）＜0对一切x∈R恒成立，即（a-2）x2+2（a-2）x-4＜0对一切x∈R恒成立，
①当a-2=0，即a=2时，-4＜0对x∈R恒成立，
∴a=2满足题意；
②当
，解得-2＜a＜0．
综合①②，可得-2＜a＜0或a=2，
故若f（x）＜0对一切x∈R恒成立，实数a的取值范围为（-2，0）∪{2}．
∴f（x）≥-1，即x2+2x-4≥-1，即x2+2x-3≥0，
∴x≤-3或x≥1，
∴关于x的不等式f（x）≥-1的解集为{x|x≤-3或x≥1}；
（2）f（x）＜0对一切x∈R恒成立，即（a-2）x2+2（a-2）x-4＜0对一切x∈R恒成立，
①当a-2=0，即a=2时，-4＜0对x∈R恒成立，
∴a=2满足题意；
②当
|
综合①②，可得-2＜a＜0或a=2，
故若f（x）＜0对一切x∈R恒成立，实数a的取值范围为（-2，0）∪{2}．
练习册系列答案
阅读快车系列答案
相关题目
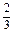＞0;(2)9x2-6x+1≥0.
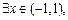使不等式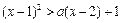
成立；命题q：
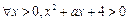恒成立．已知p或q为真，求实数a的取值范围．
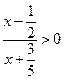的解集是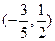
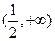
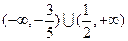
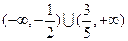
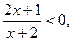判断方程
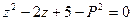有