题目内容
已知mx2+mx+m<1的解集为R,则m的取值范围是( )
| A.(-∞,0) | B.(-∞,0)∪(
| C.(-∞,0] | D.(-∞,0]∪[
|
①当m=0时,mx2+mx+m<1化为0<1,其解集为R,满足条件;
②当m≠0时,要使mx2+mx+m-1<0的解集为R,必须满足
,解得m<0.
综上可知:m的取值范围是(-∞,0].
故选C.
②当m≠0时,要使mx2+mx+m-1<0的解集为R,必须满足
|
综上可知:m的取值范围是(-∞,0].
故选C.

练习册系列答案
相关题目
 的不等式
的不等式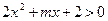
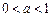 ,则不等式
,则不等式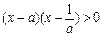 的解集为( )
的解集为( )
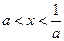
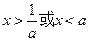
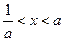
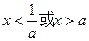
 +
+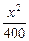 (n为常数,且n∈N).
(n为常数,且n∈N).