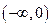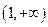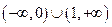题目内容
（本小题满分12分）（1）解关于x的不等式：(x – 1)2>a(x – 2) + 1(a∈R)．
（2）命题p：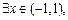
使不等式
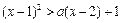成立；命题q：
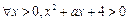恒成立．已知p或q为真，求实数a的取值范围．
（2）命题p：
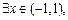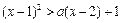使不等式成立；命题q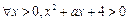：恒成立．已知p或q为真，求实数a的取值范围． (Ⅰ)略 (Ⅱ) (–4，+∞)
（1）由(x – 1)2>a(x – 2) + 1得x2 – (2 + a)x + 2a >0
即(x – 2)(x –a) >0…………（3分）
当a >2时，原不等式的解集为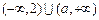
；………（4分）
当a = 2时，原不等式的解集为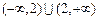
；……（5分）
当a<2时，原不等式的解集为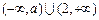
．（6分）
（2）由（1）可知命题p为真即a>–1；…（8分）
由x2 + ax + 4>0得a > –x –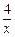
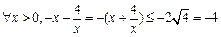
∴a >–4…（10分）由p或q为真可知a的取值范围是(–4，+∞) ……（12分）
即(x – 2)(x –a) >0…………（3分）
当a >2时，原不等式的解集为
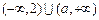；………（4分）当a = 2时，原不等式的解集为
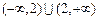；……（5分）当a<2时，原不等式的解集为
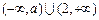．（6分）（2）由（1）可知命题p为真即a>–1；…（8分）
由x2 + ax + 4>0得a > –x –
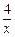
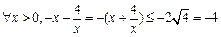
∴a >–4…（10分）由p或q为真可知a的取值范围是(–4，+∞) ……（12分）
练习册系列答案
中考解读考点精练系列答案
相关题目
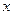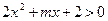
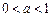的不等式
，则不等式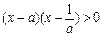
的解集为（ ）
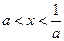
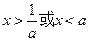
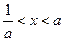
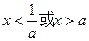
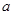是实数，试解关于
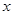的不等式：
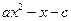＞0的解集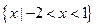
，则函数y＝f（－x）的图象为（ ）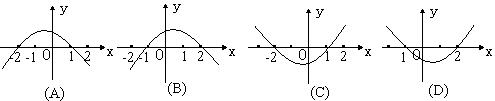
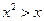的解集是
