题目内容

（2010•潍坊三模）已知圆心在x轴正半轴上的圆C过双曲线x2-y2=l的右顶点，且被双曲线的一条渐近线截得的弦长为2
7
，则圆C的方程为（　　）
分析：由圆心在x轴正半轴上的圆C过双曲线x2-y2=l的右顶点，设圆心C（x0，0）（x0＞0），双曲线x2-y2=l的右顶点A（1，0），双曲线的一条渐近线方程是x=y，圆C被双曲线的一条渐近线截得的弦长为2
7
，知(x0-1)2-7=
x02
2
，由此能求出圆C的方程．
解答：解：∵圆心在x轴正半轴上的圆C过双曲线x2-y2=l的右顶点，
∴设圆心C（x0，0）（x0＞0），
∵双曲线x2-y2=l的右顶点A（1，0），双曲线的一条渐近线方程是x=y，
∴圆C的半径r=
( x0 -1)2
，圆心C（x0，0）到渐近线x=y的距离d=
|x0|
2
，
∵圆C被双曲线的一条渐近线截得的弦长为2
7
，
∴(x0-1)2-7=
x02
2
，
解得x0=6，或x0=-2（舍），
∴圆心C（6，0），半径r=|CA|=5，
∴圆C的方程（x-6）2+y2=25．
故选C．
点评：本题主要考查双曲线标准方程，简单几何性质，直线与双曲线的位置关系，圆的简单性质等基础知识．考查运算求解能力，推理论证能力；考查化归与转化思想．解题时要认真审题，注意点到直线距离公式的灵活运用．
练习册系列答案
相关题目
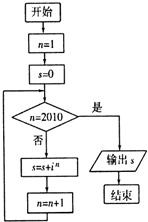（2010•潍坊三模）已知椭圆x2+4y2=4与双曲线x2-2y2=a（a＞0）的焦点重合，则该双曲线的离心率等于（　　）
（2010•潍坊三模）运行如图所示的程序框图输出的结果是（其中i是虚数单位）（　　）
（2010•潍坊三模）下列类比推理命题（R为实数集，C为复数集）：
①“若a，b∈R，则a-b=0⇒a=b”类比推出“若a，b∈C，则a-b=0⇒a=b”；
②“若a，b∈R，则a-b＞0⇒a＞b”类比推出“若a，b∈C，则a-b＞0⇒a＞b”；
③“若a，b∈R，则（a+b）（a-b）=a2-b2”类比推出“若a，b∈C，则（a+b）（a-b）=a2-b2”；
④“若a，b∈R，则|a|=|b|⇒a=±b”类比推出“若a，b∈C，则|a|=|b|⇒a=±b”．
其中类比结论正确的个数是（　　）
（2010•潍坊三模）上海世博会期间，甲、乙等六名志愿者被分配到A、B、C、D四个不同的岗位服务，每个岗位至少一名志愿者，则甲、乙两人各自独立承担一个岗位工作的分配方法共有（　　）
（2010•潍坊三模）若将函数f(x)=tan(ωx+
π
4
)(0＜ω＜1)的图象向右平移
π
6
个单位长度后与函数  g(x)=tan(ωx+
π
6
)的图象重合，则函数y=f（x）的一个对称中心为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网