题目内容
(2010•潍坊三模)若将函数f(x)=tan(ωx+
)(0<ω<1)的图象向右平移
个单位长度后与函数 g(x)=tan(ωx+
)的图象重合,则函数y=f(x)的一个对称中心为( )
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
分析:根据图象的平移求出平移后的函数解析式,与函数y=tan(ωx+
)的图象重合,比较系数,求出ω=6k+
(k∈Z),然后代入已知函数解析式中可求
| π |
| 6 |
| 1 |
| 2 |
解答:解:y=tan(ωx+
),向右平移
个单位可得:y=tan[ω(x-
)+
]=tan(ωx+
)
∴
-
ω+kπ=
∴ω=6k+
(k∈Z),
又∵1>ω>0
∴当k=0时,ω=
,f(x)=tan(
x+
)
令
x+
=
,k∈Z可得x=kπ-
π,k∈Z
当k=1时,x=
π,一个对称中心(
π,0)
故选B
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
∴
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
∴ω=6k+
| 1 |
| 2 |
又∵1>ω>0
∴当k=0时,ω=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
令
| 1 |
| 2 |
| π |
| 4 |
| kπ |
| 2 |
| 1 |
| 2 |
当k=1时,x=
| 1 |
| 2 |
| 1 |
| 2 |
故选B
点评:本题主要考查了三角函数的图象的平移,正切函数的对称性质的考查,属于三角函数性质的简单应用.

练习册系列答案
相关题目
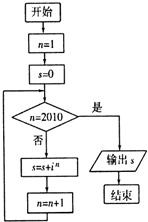 (2010•潍坊三模)运行如图所示的程序框图输出的结果是(其中i是虚数单位)( )
(2010•潍坊三模)运行如图所示的程序框图输出的结果是(其中i是虚数单位)( )