题目内容
已知函数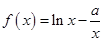 ,其中
,其中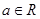 .
.
(1)当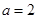 时,求函数
时,求函数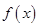 的图象在点
的图象在点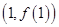 处的切线方程;
处的切线方程;
(2)如果对于任意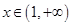 ,都有
,都有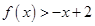 ,求
,求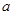 的取值范围.
的取值范围.
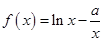 ,其中
,其中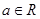 .
.(1)当
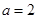 时,求函数
时,求函数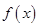 的图象在点
的图象在点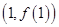 处的切线方程;
处的切线方程;(2)如果对于任意
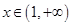 ,都有
,都有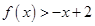 ,求
,求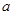 的取值范围.
的取值范围.(1)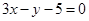 ;(2)
;(2)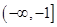 .
.
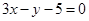 ;(2)
;(2)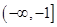 .
.试题分析:(1)将
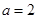 代入函数解析式,求出
代入函数解析式,求出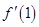 及
及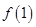 的值,利用点斜式写出切线方程;(2)利用参数分离法将
的值,利用点斜式写出切线方程;(2)利用参数分离法将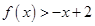 转化为
转化为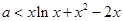 ,构造新函数
,构造新函数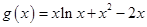 ,问题转化为
,问题转化为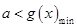 来求解,但需注意区间
来求解,但需注意区间 端点值的取舍.
端点值的取舍.试题解析:(1)由
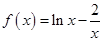 ,得
,得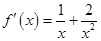 ,
,所以
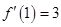 ,
,又因为
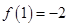 ,
,所以函数
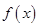 的图象在点
的图象在点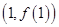 处的切线方程为
处的切线方程为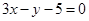 ;
;(2)由
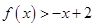 ,得
,得 ,
,即
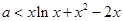 .
.设函数
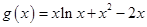 ,
,则
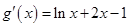 ,
,因为
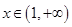 ,
,所以
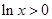 ,
,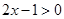 ,
,所以当
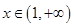 时,
时,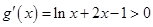 ,
,故函数
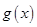 在
在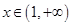 上单调递增,
上单调递增,所以当
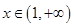 时,
时,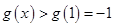 ,
,因为对于任意
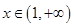 ,都有
,都有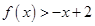 成立,
成立,所以对于任意
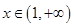 ,都有
,都有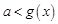 成立.
成立.所以
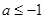 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?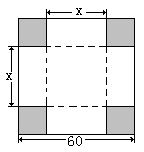
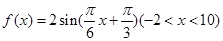 的图像与
的图像与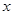 轴交于点
轴交于点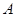 ,过点
,过点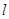 与函数
与函数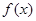 的图像交于
的图像交于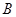
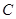 两点,则
两点,则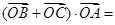 ( )
( )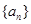 中的是函数
中的是函数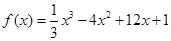 的极值点,则
的极值点,则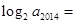
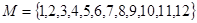 ,以下命题正确的序号是 .
,以下命题正确的序号是 .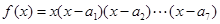 ,其中
,其中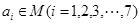 ,那么
,那么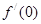 的最大值为
的最大值为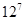 。
。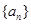 满足首项
满足首项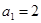 ,
,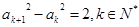 ,当
,当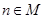 且
且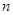 最大时,数列
最大时,数列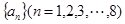 满足
满足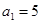 ,
,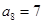 ,
,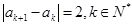 ,如果数列
,如果数列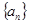 一共有33个。
一共有33个。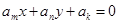 ,其中
,其中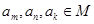 ,而且
,而且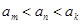 ,则一共可以得到不同的直线196条。
,则一共可以得到不同的直线196条。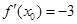 ,则
,则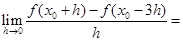 ( )
( )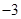
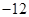
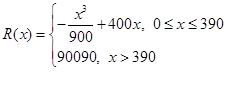 ,则当总利润最大时,每年生产产品的单位数是( )
,则当总利润最大时,每年生产产品的单位数是( )