题目内容
【题目】综合题。
（1）已知a，b∈（0，+∞），求证：x，y∈R，有 
≥ 
；
（2）若0＜a＜2，0＜b＜2，0＜c＜2，求证：（2﹣a）b，（2﹣b）c，（2﹣c）a不能同时大于1．
【答案】
（1）证明：（ 
）（a+b）=x2+ 
+y2≥x2+2xy+y2=（x+y）2，
当且仅当 ，即|bx|=|ay|时取等号，
由于a，b∈（0，+∞），所以有 ≥ 
（2）证明：假设结论不成立，即（2﹣a）b，（2﹣b）c，（2﹣c）a同时大于1．
，
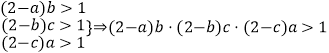而（2﹣a）b（2﹣b）c（2﹣c）a=（2﹣a）a（2﹣b）b（2﹣c）c
≤（ 
）2（ 
）2（ 
）2=1，
这与（2﹣a）b（2﹣b）c（2﹣c）a＞1矛盾．
所以假设错误，即（2﹣a）b，（2﹣b）c，（2﹣c）a不能同时大于1
【解析】（1）由基本不等式易得答案，注意取等条件|bx|=|ay|；（2）假设（2﹣a）b，（2﹣b）c（2﹣c）a同时大于1，推出（2﹣a）b（2﹣b）c（2﹣c）a＞1 ①；再由已知条件可推出（2﹣a）b（2﹣b）c（2﹣c）a≤1，这与①矛盾，故假设不成立，即可得出结论．
【考点精析】利用反证法与放缩法对题目进行判断即可得到答案，需要熟知常见不等式的放缩方法：①舍去或加上一些项②将分子或分母放大（缩小)．
练习册系列答案
字词句篇与同步作文达标系列答案
走进文言文系列答案
相关题目
