题目内容
6.偶函数f(x)满足?x∈R,f(x+2)=f(2-x),f(3)=3,则f(2015)=3.分析 由已知分析出函数f(x)是周期为4的周期函数,可得f(2015)=f(3)=3.
解答 解:∵偶函数f(x)满足?x∈R,f(x+2)=f(2-x),
∴f(x+4)=f[(x+2)+2]=f[2-(x+2)]=f(-x)=f(x),
故函数f(x)是周期为4的周期函数,
故f(2015)=f(3)=3,
故答案为:3
点评 本题考查的知识点是函数奇偶性,函数的对称性,函数的周期性,是函数图象和性质的综合应用.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
18.已知全集U={x||x|≤2},A={x|x2+x-2≤0},则∁UA=( )
| A. | {x|1≤x≤2} | B. | {x|1<x≤2} | C. | {x|-1≤x≤2} | D. | {x|-1<x≤2} |
18.函数y=$\sqrt{{x}^{2}-4x+13}$-$\sqrt{{x}^{2}+1}$的最大值是( )
| A. | 2$\sqrt{2}$ | B. | 10 | C. | $\sqrt{10}$ | D. | 0 |
15.下列说法正确的是( )
| A. | 命题“若幂函数f(x)=xa在(0,+∞)内单调递减,则 a<0”的逆否命题是“若a≥0,则幂函数f(x)=xa在(0,+∞)内单调递增” | |
| B. | 已知命题p 和q,若p∧q为假命题,则命题p、q中必有一个是真命题、一个是假命题 | |
| C. | 若x,y∈R,则“x=y”是“$xy≥{(\frac{x+y}{2})^2}$”的充要条件 | |
| D. | 若命题p:?x0∈R,x02+x0+1<0,则¬p:?x∈R,x2+x+1>0 |
11.已知数列{an},若点(n,an)(n∈N+)均在直线y-3=k(x-6)上,则数列{an}的前11项和S11等于( )
| A. | 18 | B. | 22 | C. | 33 | D. | 44 |
15.设θ是第三象限角,|cos$\frac{θ}{2}$|=cos$\frac{θ}{2}$,则$\frac{θ}{2}$是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 的首项
的首项 ,前
,前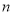 项和为
项和为 ,且
,且 ,则数列
,则数列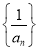 的前5项和为( )
的前5项和为( ) B.
B.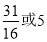 C.
C. D.
D.