(2012•丰台区二模)一个正四棱锥的所有棱长均为2.其俯视图如图所示.则该正四棱锥的正视图的面积为( )A．2B．3C．2D．4 题目和参考答案——青夏教育精英家教网—

题目内容

（2012•丰台区二模）一个正四棱锥的所有棱长均为2，其俯视图如图所示，则该正四棱锥的正视图的面积为（　　）

A．

B．

C．2

D．4

分析：本题先要把原几何体画出来，再求出棱锥的高PO=

，它就是正视图中的高，而正视图的底边就等于BC=2，由三角形的面积公式可得答案．

解答：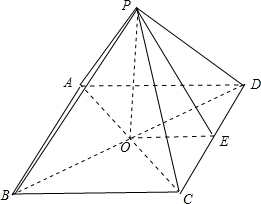

解：由题意可知，原几何体如上图，其中，OE=1，PE=

，在RT△POE中，PO=

，
故所得正视图为底边为2，高为

的三角形，
故其面积S=

×2×

故选A

点评：本题为三视图的还原问题，要注意前后量的联系，知道正视图为三角形，故只需求底和高，而高就是棱锥的高，属基础题．

练习册系列答案

相关题目

（2012•丰台区二模）执行如图所示的程序框图，若输出的结果为63，则判断框中应填（　　）

（2012•丰台区二模）如图所示，四棱锥P-ABCD中，底面ABCD是边长为2的菱形，Q是棱PA上的动点．
（Ⅰ）若Q是PA的中点，求证：PC∥平面BDQ；
（Ⅱ）若PB=PD，求证：BD⊥CQ；
（Ⅲ）在（Ⅱ）的条件下，若PA=PC，PB=3，∠ABC=60°，求四棱锥P-ABCD的体积．

（2012•丰台区二模）从5名学生中任选4名分别参加数学、物理、化学、生物四科竞赛，且每科竞赛只有1人参加，若甲不参加生物竞赛，则不同的选择方案共有

种．

（2012•丰台区二模）在平面直角坐标系中，若点A，B同时满足：①点A，B都在函数y=f（x）图象上；②点A，B关于原点对称，则称点对（A，B）是函数y=f（x）的一个“姐妹点对”（规定点对（A，B）与点对（B，A）是同一个“姐妹点对”）．那么函数f(x)=

x-4，	x≥0
x2-2x，	x＜0

的“姐妹点对”的个数为

；当函数g（x）=a^x-x-a有“姐妹点对”时，a的取值范围是

a＞1

．

（2012•丰台区二模）某地区恩格尔系数y（%）与年份x的统计数据如下表：

年份x	2004	2005	2006	2007
恩格尔系数y（%）	47	45.5	43.5	41

从散点图可以看出y与x线性相关，且可得回归方程为

x+4055.25，据此模型可预测2012年该地区的恩格尔系数（%）为

31.25

．

试题分类