题目内容
（2012•丰台区二模）在平面直角坐标系中，若点A，B同时满足：①点A，B都在函数y=f（x）图象上；②点A，B关于原点对称，则称点对（A，B）是函数y=f（x）的一个“姐妹点对”（规定点对（A，B）与点对（B，A）是同一个“姐妹点对”）．那么函数f(x)=
的“姐妹点对”的个数为
|
1
1
；当函数g（x）=ax-x-a有“姐妹点对”时，a的取值范围是a＞1
a＞1
．分析：第一空：欲求f（x）的“姐妹点对”，只须作出函数y=x-4（x≥0）的图象关于原点对称的图象，观察它与函数y=x2-2x（x＜0）交点个数即可．
第二空：构建函数y=ax（a＞0，且a≠1）和函数y=x+a，函数y=ax（a＞0，且a≠1）关于原点对称的函数为y=-a-x，函数f（x）=ax-x-a（a＞0且a≠1）只有一个“姐妹点对”，可转化为函数y=x+a与y=-a-x只有一个交点，由此可得结论．
第二空：构建函数y=ax（a＞0，且a≠1）和函数y=x+a，函数y=ax（a＞0，且a≠1）关于原点对称的函数为y=-a-x，函数f（x）=ax-x-a（a＞0且a≠1）只有一个“姐妹点对”，可转化为函数y=x+a与y=-a-x只有一个交点，由此可得结论．
解答：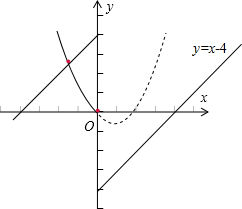
解：根据题意可知，欲求f（x）的“姐妹点对”，只须作出函数y=x-4（x≥0）的图象关于原点对称的图象，观察它与函数y=x2-2x（x＜0）交点个数即可．
函数y=x-4（x≥0）关于原点对称的函数为y=x+4（x＜0）
在同一坐标系作出函数的图象，观察图象可得：它们的交点个数是：1．
即f（x）的“姐妹点对”有：1个．
故答案为：1
当函数g（x）=ax-x-a有“姐妹点对”时：构建函数y=ax（a＞0，且a≠1）和函数y=x+a，函数y=ax（a＞0，且a≠1）关于原点对称的函数为y=-a-x
∵函数f（x）=ax-x-a（a＞0且a≠1）只有一个“姐妹点对”，
∴函数y=x+a与y=a-x只有一个交点
∵a＞1时，y=a-x单调减，与函数y=x+a图象只有一个交点；
0＜a＜1时，y=a-x单调减，与函数y=x+a图象没有交点；
此时有a＞1；
故答案为a＞1．
解：根据题意可知，欲求f（x）的“姐妹点对”，只须作出函数y=x-4（x≥0）的图象关于原点对称的图象，观察它与函数y=x2-2x（x＜0）交点个数即可．函数y=x-4（x≥0）关于原点对称的函数为y=x+4（x＜0）
在同一坐标系作出函数的图象，观察图象可得：它们的交点个数是：1．
即f（x）的“姐妹点对”有：1个．
故答案为：1
当函数g（x）=ax-x-a有“姐妹点对”时：构建函数y=ax（a＞0，且a≠1）和函数y=x+a，函数y=ax（a＞0，且a≠1）关于原点对称的函数为y=-a-x
∵函数f（x）=ax-x-a（a＞0且a≠1）只有一个“姐妹点对”，
∴函数y=x+a与y=a-x只有一个交点
∵a＞1时，y=a-x单调减，与函数y=x+a图象只有一个交点；
0＜a＜1时，y=a-x单调减，与函数y=x+a图象没有交点；
此时有a＞1；
故答案为a＞1．
点评：本题考查新定义，考查函数的对称性，以及数形结合的思想，解答的关键在于对“姐妹点对”的正确理解，合理地利用图象法解决．考查学生分析转化问题的能力，属于中档题．
练习册系列答案
相关题目
（2012•丰台区二模）执行如图所示的程序框图，若输出的结果为63，则判断框中应填（ ）
（2012•丰台区二模）如图所示，四棱锥P-ABCD中，底面ABCD是边长为2的菱形，Q是棱PA上的动点．