题目内容
设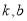
均为非零常数，给出如下三个条件：
①
与
均为等比数列；
②为等差数列，为等比数列；
③为等比数列，为等差数列，
其中一定能推导出数列为常数列的是（ ）
A．①② B．①③ C．②③ D．①②③
练习册系列答案
相关题目
题目内容
设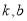均为非零常数，给出如下三个条件：
①与均为等比数列；
②为等差数列，为等比数列；
③为等比数列，为等差数列，
其中一定能推导出数列为常数列的是（ ）
A．①② B．①③ C．②③ D．①②③
为奇函数，当
时，
，则当
时，
____.
，
．
，
；
，若
，求实数
的取值集合．
满足
，对于任意
都有
，且
，令
．
的表达式；
在区间
上有两个零点，求
的取值范围．
在定义域的某个子区间
上不具有单调性，则实数
的取值范围为 ．
，则（ ）
B．
C．
D．
中，已知
分别是棱
的中点，若
，设
，则
的最大值是 ．
与圆
相切于点
，
是过点
，点
是线段
的中点．
四点共圆；
．
B．