题目内容
函数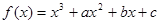 ,过曲线
,过曲线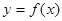 上的点
上的点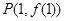 的切线方程为
的切线方程为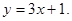 .
.
(1)若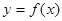 在
在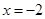 时有极值,求
时有极值,求 的表达式;
的表达式;
(2)在(1)的条件下,求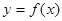 在[-3,1]上的最大值;
在[-3,1]上的最大值;
(3)若函数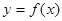 在区间[-2,1]上单调递增,求实数b的取值范围.
在区间[-2,1]上单调递增,求实数b的取值范围.
(1) ;(2)13;(3)
;(2)13;(3)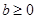 .
.
解析试题分析:(1)题目条件给出了关于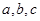 的两组关系,第一问中又给出了一组关系,所以在第一问很容易就能将表达式求出;(2)我们求解无参函数在定区间上的最大值,只需求导看
的两组关系,第一问中又给出了一组关系,所以在第一问很容易就能将表达式求出;(2)我们求解无参函数在定区间上的最大值,只需求导看 在
在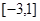 上的单调性,然后找到极小值就是最小值,最大值通过比较端点值即可判断出;(3)考查函数单调性的问题,我们可以将其转化为不等式恒成立问题,转化之后的不等式是比较常见的二次不等式恒成立,一般碰到这种问题我们采取分离参数的方法将参数分到一边,求出另一边的最值即可,另一边的函数是常见的对勾函数,在这里区间给的比较好,可以让我们用基本不等式解出最大值,然后参数大于最大值即可.
上的单调性,然后找到极小值就是最小值,最大值通过比较端点值即可判断出;(3)考查函数单调性的问题,我们可以将其转化为不等式恒成立问题,转化之后的不等式是比较常见的二次不等式恒成立,一般碰到这种问题我们采取分离参数的方法将参数分到一边,求出另一边的最值即可,另一边的函数是常见的对勾函数,在这里区间给的比较好,可以让我们用基本不等式解出最大值,然后参数大于最大值即可.
试题解析:(1)由 得
得 ,过
,过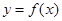 上点
上点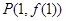 的切线方
的切线方
程为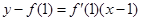 ,即
,即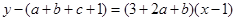 .而过
.而过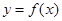 上点
上点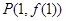 的切
的切
线方程为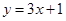 ,故
,故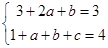 即
即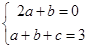 ,∵
,∵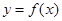 在
在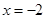 处有极值,
处有极值,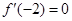 ,
,
∴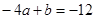 ,联立解得
,联立解得 .∴
.∴ .
.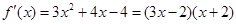 ,令
,令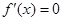 得
得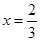 或
或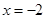 ,列下表:
,列下表:
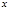 | 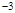 | 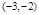 | 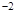 | 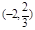 | 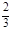 | 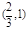 | 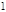 |
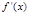 | | 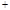 | |  | | 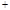 | |
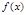 | 
练习册系列答案
 黄冈天天练口算题卡系列答案 黄冈天天练口算题卡系列答案
相关题目
|

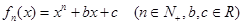
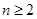 ,
,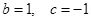 ,证明:
,证明: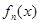 在区间
在区间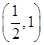 内存在唯一的零点;
内存在唯一的零点;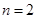 ,若对任意
,若对任意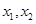
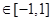 ,有
,有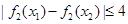 ,求
,求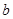 的取值范围
的取值范围 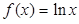 .
.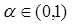 ,求
,求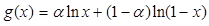 最大值;
最大值;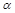 ,
,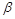 满足
满足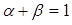 .求证:
.求证: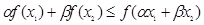 ;
;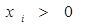 ,正数
,正数 满足
满足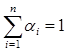 .证明:
.证明: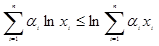
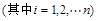 .
.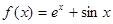 ,
,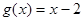 ;
;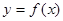 在
在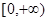 上单调递增;
上单调递增;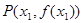 ,
,
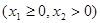 ,若直线
,若直线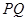
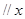 轴,求
轴,求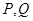 两点间的最短距离.
两点间的最短距离.  和
和 是函数
是函数 的两个极值点,其中
的两个极值点,其中 ,
, .
. 的取值范围;
的取值范围; ,求
,求 的最大值.注:e是自然对数的底.
的最大值.注:e是自然对数的底. 满足:在定义域内存在实数
满足:在定义域内存在实数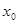 ,使
,使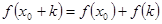 (k为常数),则称“f(x)关于k可线性分解”.
(k为常数),则称“f(x)关于k可线性分解”.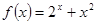 是否关于1可线性分解?请说明理由;
是否关于1可线性分解?请说明理由;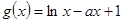
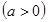 关于
关于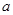 可线性分解,求
可线性分解,求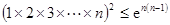
 .
.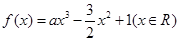 ,其中
,其中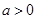 .
. ,求曲线
,求曲线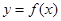 在点
在点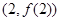 处的切线方程;
处的切线方程; 有三个零点,求
有三个零点,求 的取值范围.
的取值范围.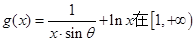 上为增函数,且
上为增函数,且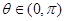 ,
,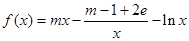 ,
,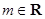 .
.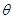 的值;
的值;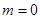 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值;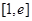 上至少存在一个
上至少存在一个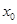 ,使得
,使得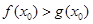 成立,求
成立,求 的取值范围.
的取值范围. ,
, .
. 的单调性;
的单调性; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.