题目内容
在棱长为 的正方体
的正方体 中,
中, 、
、 分别是
分别是 、
、 的中点,求点
的中点,求点 到截面
到截面 的距离 .
的距离 .
 的正方体
的正方体 中,
中, 、
、 分别是
分别是 、
、 的中点,求点
的中点,求点 到截面
到截面 的距离 .
的距离 .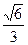
以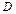 为原点,建立如图所示的空间直角坐标系.
为原点,建立如图所示的空间直角坐标系.

则 .
.
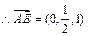 ,
,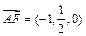 ;
;
设面 的法向量为
的法向量为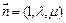 ,
,
则有: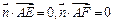 ,
,
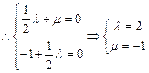 ,
,
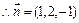 ,又
,又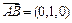 ,所以点
,所以点 到截面
到截面 的距离为
的距离为 =
=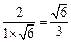 .
.
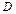 为原点,建立如图所示的空间直角坐标系.
为原点,建立如图所示的空间直角坐标系.
则
 .
.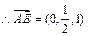 ,
,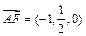 ;
;设面
 的法向量为
的法向量为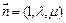 ,
,则有:
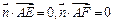 ,
,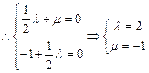 ,
,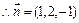 ,又
,又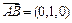 ,所以点
,所以点 到截面
到截面 的距离为
的距离为 =
=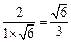 .
.
练习册系列答案
相关题目
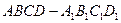 的棱长为
的棱长为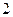 ,
,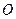 是
是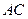 与
与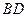 的交点,
的交点,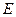 是
是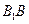 上一点,且
上一点,且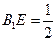 .(Ⅰ)求证:
.(Ⅰ)求证: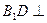 平面
平面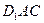 ;
;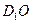 与
与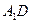 所成角的余弦值;
所成角的余弦值;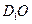 与平面
与平面 所成角的正弦值.
所成角的正弦值.
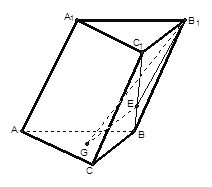
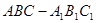 中,侧面
中,侧面 ,
,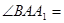
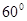 ,
,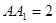 ,底面
,底面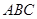 是边长为
是边长为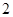 的正三角形,其重心为
的正三角形,其重心为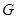 点,
点,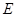 是线段
是线段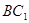 上一点,且
上一点,且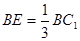 .
.
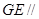 侧面
侧面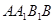 ;
;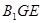 与底面
与底面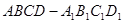 中,
中,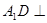 平面
平面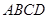 ,底面
,底面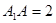 ,
,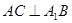 ;
;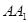 上存在一点
上存在一点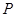 ,使得
,使得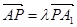 ,
,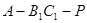 的大小为
的大小为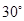 时,求实数
时,求实数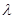 的值.
的值.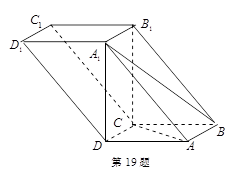
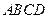 的长方体被截面
的长方体被截面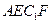 所截面而得到的,其中
所截面而得到的,其中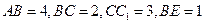 .
.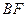 的长;
的长;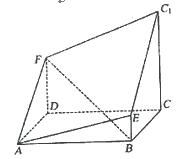
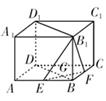
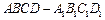 中,底面边长为
中,底面边长为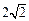 ,侧棱长为4,点
,侧棱长为4,点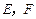 分别为棱
分别为棱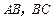 的中点,
的中点,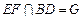 ,求点
,求点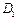 到平面
到平面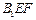 的距离
的距离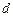 .
.
 ,
, 〉=
〉= .
.
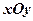 中,方程
中,方程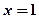 表示过点
表示过点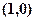 且平行于
且平行于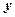 轴的直线。类比以上结论有:在空间直角坐标系
轴的直线。类比以上结论有:在空间直角坐标系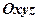 中,方程
中,方程