题目内容
12.函数f(x)=4x-3•2x+3的值域为[1,7],则f(x)的定义域为( )| A. | (-1,1)∪[2,4] | B. | (0,1)∪[2,4] | C. | [2,4] | D. | (-∞,0]∪[1,2] |
分析 设t=2x则t>0,代入原函数利用配方法化简,根据函数的值域和二次函数的性质求出t的范围,再由指数函数的性质求出x的范围,可得f(x)的定义域.
解答 解:设t=2x,则t>0,
代入原函数得:y=t2-3t+3=${(t-\frac{3}{2})}^{2}+\frac{3}{4}$≥$\frac{3}{4}$,
∵函数f(x)=4x-3•2x+3的值域为[1,7],
∴函数y=t2-3t+3的值域为[1,7],
由y=1得t=1或2,由y=7得t=4或-1(舍去),
则0<t≤1或2≤t≤4,
即0<2x≤1或2≤2x≤4,解得x<0或1≤x≤2,
∴f(x)的定义域是(-∞,0]∪[1,2],
故选:D.
点评 本题考查指数函数的性质,二次函数的性质的应用,以及换元法的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知向量$\overrightarrow{OA}$=(2,2),$\overrightarrow{OB}$=(4,1),在x轴上有一点P,使$\overrightarrow{AP}$•$\overrightarrow{BP}$有最小值,则P点坐标为( )
| A. | (-3,0) | B. | (3,0) | C. | (2,0) | D. | (4,0) |
1.tan75°=( )
| A. | 2+$\sqrt{3}$ | B. | 1+$\sqrt{3}$ | C. | $\frac{3+\sqrt{3}}{3}$ | D. | 2-$\sqrt{3}$ |
2.已知函数f(x)在R上可导,下列四个选项中正确的是( )
| A. | 若f(x)>f′(x)对x∈R恒成立,则 ef(1)<f(2) | |
| B. | 若f(x)<f′(x)对x∈R恒成立,则e2f(-1)>f(1) | |
| C. | 若f(x)+f′(x)>0对x∈R恒成立,则ef(2)<f(1) | |
| D. | 若f(x)+f′(x)<0对x∈R恒成立,则f(-1)>e2f(1) |
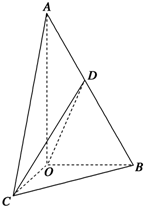 如图,在三棱锥A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=2$\sqrt{2}$,动点D在线段AB上.
如图,在三棱锥A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=2$\sqrt{2}$,动点D在线段AB上.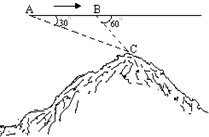 航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10000m,速度为180km/h.飞机先看到山顶的俯角为15°,经过420s后又看到山顶的俯角为450,求山顶的海拔高度(取$\sqrt{2}$=1.4,$\sqrt{3}$=1.7,$\sqrt{6}$=2.2).
航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10000m,速度为180km/h.飞机先看到山顶的俯角为15°,经过420s后又看到山顶的俯角为450,求山顶的海拔高度(取$\sqrt{2}$=1.4,$\sqrt{3}$=1.7,$\sqrt{6}$=2.2).