题目内容
函数
的单调递增区间为 ；值域为 ．
【答案】分析：将原函数 化为 u=-x2-3x+4，y=
，原函数单调递增区间 即为u（＞0）的单调递增区间．求出u的取值范围，再求y的取值范围．
解答：解：由-x2-3x+4＞≥得函数的定义域为[-4，1]，函数
的单调递增区间即为u=-x2-3x+4在[-4，1]上的调递增区间．
而u=-（x+
）2+
在 
上单增，所以原函数调递增区间为
．
而u=-（x+
）2+
[-4，1]上的值域为[0，
]，∴
∈
故答案为：
点评：本题考查复合函数的单调区间，值域求解．求解过程要注意u应大于等于0，否则会将单调递增区间及值域范围扩大．
，原函数单调递增区间 即为u（＞0）的单调递增区间．求出u的取值范围，再求y的取值范围．解答：解：由-x2-3x+4＞≥得函数的定义域为[-4，1]，函数
的单调递增区间即为u=-x2-3x+4在[-4，1]上的调递增区间．而u=-（x+
）2+ 在 上单增，所以原函数调递增区间为．而u=-（x+
）2+[-4，1]上的值域为[0，]，∴∈故答案为：
点评：本题考查复合函数的单调区间，值域求解．求解过程要注意u应大于等于0，否则会将单调递增区间及值域范围扩大．
练习册系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
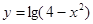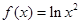的单调递增区间为________________
的单调递增区间为
。