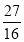Question

考虑以下数列{an}，n∈N*：①an＝n2＋n＋1；②an＝2n＋1；③an＝ln 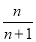.其中满足性质“对任意的正整数n，≤an＋1都成立”的数列有________(写出所有满足条件的序号)．

 

Answer 1

②③

【解析】对于①，a1＝3，a2＝7，a3＝13，>a2，因此{an}不满足性质“对任意的正整数n，≤an＋1都成立”．对于②，易知数列{an}是等差数列，故有＝an＋1，因此{an}满足性质“对任意的正整数n，≤an＋1都成立”．对于③，an＋2＋an＝ln，2an＋1＝ln，－＝＝<0，即<an＋1，因此{an}满足性质“对任意的正整数n，≤an＋1都成立 ”