题目内容
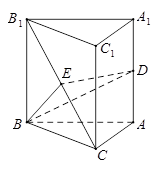
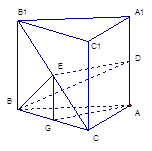
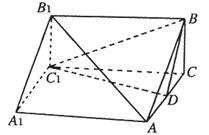
如图,在棱长都相等的正三棱柱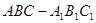 中,
中,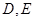 分别为
分别为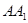 ,
,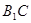 的中点.
的中点.
⑴求证: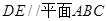 ;
;
⑵求证: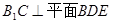 .
.
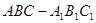 中,
中,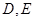 分别为
分别为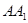 ,
,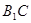 的中点.
的中点.⑴求证:
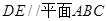 ;
; ⑵求证:
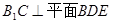 .
.
略
⑴取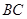 中点
中点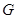 ,连结
,连结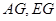 ,
,
 分别为
分别为 的中点,
的中点, 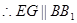 ,且
,且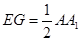
又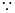 正三棱柱
正三棱柱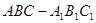 ,
,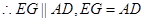
 四边形
四边形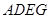 为平行四边形。
为平行四边形。
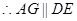
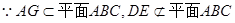
所以 .
.
⑵ 正三棱柱
正三棱柱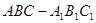 ,
,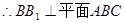 。
。
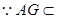 平面
平面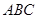 ,
,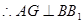 ,
,
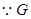 为
为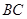 的中点,
的中点,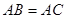 ,
, 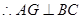
 ,
, 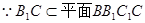
 ,
,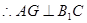
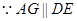
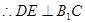 ;
; 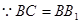 ,
,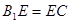
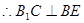
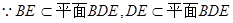
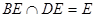
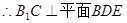 .
.
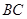 中点
中点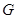 ,连结
,连结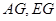 ,
,
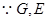 分别为
分别为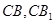 的中点,
的中点, 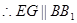 ,且
,且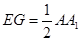
又
 正三棱柱
正三棱柱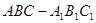 ,
,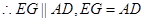
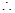 四边形
四边形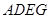 为平行四边形。
为平行四边形。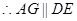
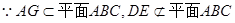
所以
 .
.⑵
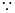 正三棱柱
正三棱柱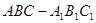 ,
,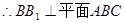 。
。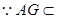 平面
平面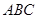 ,
,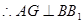 ,
,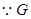 为
为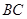 的中点,
的中点,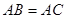 ,
, 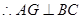
 ,
, 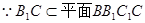
 ,
,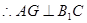
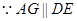
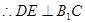 ;
; 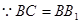 ,
,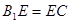
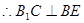
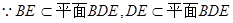
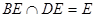
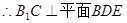 .
.
练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
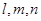 是三条不重合的直线,
是三条不重合的直线, 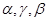 是三个不重合的平面,下列四个命题正确的个数为 ( )
是三个不重合的平面,下列四个命题正确的个数为 ( )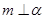 , m∥
, m∥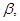
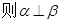
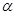 所成的角相等,则m∥n;
所成的角相等,则m∥n;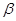 ,n∥β,则
,n∥β,则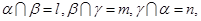
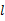 ∥
∥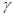 ,则m∥n.
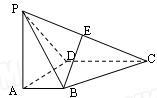
,则m∥n. PA
PA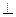 PC,D为AB中点且△PDB为正三角形
PC,D为AB中点且△PDB为正三角形 证:BC⊥平面PAC;
证:BC⊥平面PAC;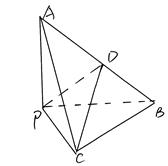
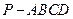 的底面
的底面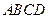 为菱形,
为菱形,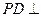 平面
平面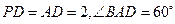 ,
, 、
、 分别为
分别为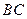 、
、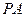 的中点。
的中点。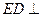 平面
平面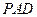 ;
; (Ⅱ)求三棱锥
(Ⅱ)求三棱锥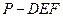 的体积;
的体积;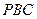 所成的锐二面角大小的余弦值。
所成的锐二面角大小的余弦值。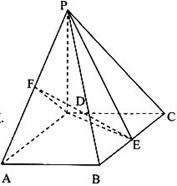
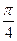 .
. 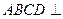 平面
平面 ;
;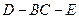 的平面角的正切值.
的平面角的正切值.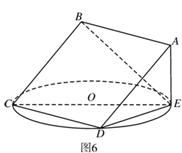
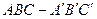 的
的 底面是边长为1cm的正三角形,侧面是长方形,侧棱长为4cm,一个小虫从A点出发沿表面一圈到达
底面是边长为1cm的正三角形,侧面是长方形,侧棱长为4cm,一个小虫从A点出发沿表面一圈到达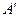 点,则小虫所行的最短路程为__________cm
点,则小虫所行的最短路程为__________cm