题目内容
18.已知圆x2+y2-4x-8y+m=0.(1)若圆C与直线x+2y-5=0相交于M、N两点,且CM⊥CN(C为圆心),求m的值;
(2)在(1)的条件下,求以MN为直径的圆的方程.
分析 (1)CM⊥CN(C为圆心),可得圆心到直线的距离d=$\frac{\sqrt{2}}{2}$r,即可求m的值;
(2)过C与直线x+2y-5=0垂直的直线方程为2x-y=0,与直线x+2y-5=0交点为(1,2),即为圆心,求出半径,即可求以MN为直径的圆的方程.
解答 解:(1)圆x2+y2-4x-8y+m=0可化为圆(x-2)2+(y-4)2=20-m,
∵圆C与直线x+2y-5=0相交于M、N两点,且CM⊥CN(C为圆心),
∴圆心到直线的距离d=$\frac{|2+8-5|}{\sqrt{5}}$=$\frac{\sqrt{2}}{2}•\sqrt{20-m}$,
∴m=10;
(2)过C与直线x+2y-5=0垂直的直线方程为2x-y=0,与直线x+2y-5=0交点为(1,2),即为圆心,
∵|MN|=2$\sqrt{5}$,
∴以MN为直径的圆的方程为(x-1)2+(y-2)2=5.
点评 本题考查圆的方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
3.不等式组$\left\{\begin{array}{l}{{x}^{2}-1<0}\\{{x}^{2}-3x>0}\end{array}\right.$的解集是( )
| A. | {x|-1<x<1} | B. | {x|-1<x<0} | C. | {x|0<x<1} | D. | {x|0<x<3} |
7.已知幂函数f(x)的图象经过点($\sqrt{3}$,3),则f(2)的值是( )
| A. | 4 | B. | 2 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
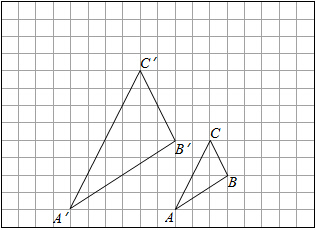 如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上. 在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=1,AD=2,PA⊥底面ABCD,PD与底面成30°角.
在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=1,AD=2,PA⊥底面ABCD,PD与底面成30°角.