题目内容
若数列{an}的前n项和Sn=2n2-3n+2,则它的通项公式an是______.
当n=1时,
a1=S1=2-3+2=1.
当n≥2时,
an=Sn-Sn-1=2n2-3n+2-[2(n-1)2-3(n-1)+2]=4n-5.
∴an=
.
故答案为an=
.
a1=S1=2-3+2=1.
当n≥2时,
an=Sn-Sn-1=2n2-3n+2-[2(n-1)2-3(n-1)+2]=4n-5.
∴an=
|
故答案为an=
|

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 ,则
,则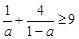
 ,则下列推证中正确的是( )
,则下列推证中正确的是( )

 ,
,