题目内容
如图是一个直三棱柱(以A1B1C1为底面)被一平面
所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,
AAl=4,BBl=2,CCl=3,且设点O是AB的中点。
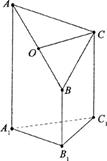
(1)证明:OC∥平面A1B1C1;
(2)求异面直线OC与AlBl所成角的正切值。
所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,
AAl=4,BBl=2,CCl=3,且设点O是AB的中点。

(1)证明:OC∥平面A1B1C1;
(2)求异面直线OC与AlBl所成角的正切值。
(1)证明:作OD∥AA1交A1B1于D,连C1D,得到OD∥BB1∥CC1 ,
因为O是AB的中点,可证ODCC1是平行四边形,因此有OC∥C1D,推出OC∥面A1B1C1 ;
(2)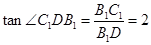 。
。
因为O是AB的中点,可证ODCC1是平行四边形,因此有OC∥C1D,推出OC∥面A1B1C1 ;
(2)
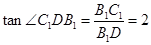 。
。试题分析:(1)证明:作OD∥AA1交A1B1于D,连C1D
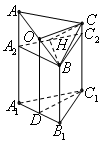
则OD∥BB1∥CC1
因为O是AB的中点,
所以
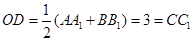
则ODCC1是平行四边形,因此有OC∥C1D
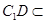 平面C1B1A1且
平面C1B1A1且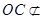 平面C1B1A1,
平面C1B1A1,则OC∥面A1B1C1 6分
(2)由(1)得OC∥C1D,则
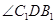 为异面直线OC与AlBl所成角。
为异面直线OC与AlBl所成角。在
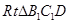 中,
中,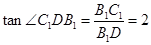 12分
12分点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,如果利用空间向量,可省去繁琐的证明,也是解决立体几何问题的一个基本思路。注意运用转化与化归思想,将空间问题转化成平面问题。

练习册系列答案
相关题目
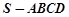 中,底面
中,底面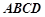 是直角梯形,
是直角梯形,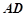 ∥
∥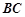 ,
,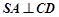 ,
,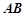 ⊥平面SAD,点
⊥平面SAD,点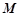 是
是 的中点,且
的中点,且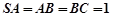 ,
,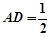 .
. 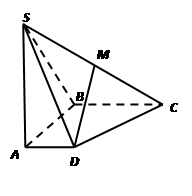
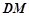 ∥平面
∥平面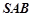 ;
; 与平面
与平面 ,有以下四个命题:
,有以下四个命题: 且
且 ,则
,则 ; ②若
; ②若 且
且 ,则
,则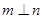 ;
; 且
且 且
且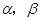 ,直线
,直线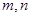 ,下列命题中不正确的是 ( )
,下列命题中不正确的是 ( )



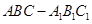 中,四边形
中,四边形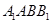 是正方形,
是正方形,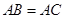 ,
,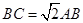 ,
,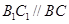 且
且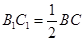 ,二面角
,二面角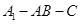 是直二面角
是直二面角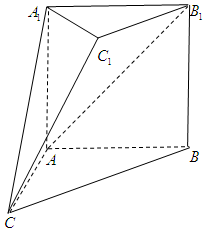
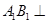 平面
平面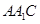 ;
;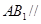 平面
平面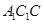 。
。 为空间四边形
为空间四边形 的边
的边 上的点,且
上的点,且 ,求证:
,求证: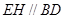 .
.
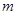 ,
,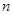 与两个不同的平面
与两个不同的平面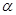 ,
,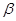 ,下列正确的是( )
,下列正确的是( )  且
且 ,则
,则
 且
且 ,则
,则
 且
且
 且
且 为矩形,
为矩形, 为直角梯形,且
为直角梯形,且 =
=  = 90°,平面
= 90°,平面 平面
平面 ,
,

 为
为 的中点,求证:
的中点,求证: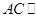 平面
平面 ;
; 与平面
与平面 所成锐二面角的大小.
所成锐二面角的大小.