题目内容
如图所示的几何体中,四边形 为矩形,
为矩形, 为直角梯形,且
为直角梯形,且 =
=  = 90°,平面
= 90°,平面 平面
平面 ,
, ,
,

(1)若 为
为 的中点,求证:
的中点,求证: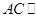 平面
平面 ;
;
(2)求平面 与平面
与平面 所成锐二面角的大小.
所成锐二面角的大小.
 为矩形,
为矩形, 为直角梯形,且
为直角梯形,且 =
=  = 90°,平面
= 90°,平面 平面
平面 ,
, ,
,

(1)若
 为
为 的中点,求证:
的中点,求证: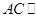 平面
平面 ;
;(2)求平面
 与平面
与平面 所成锐二面角的大小.
所成锐二面角的大小.(Ⅰ)连结 ,交
,交 与
与 ,连结
,连结 ,
,
 中,
中, 分别为两腰
分别为两腰 的中点 , 确定
的中点 , 确定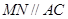 .
.
得到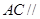 平面
平面 .
.
(Ⅱ)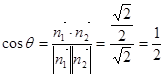 ,
, .
.
 ,交
,交 与
与 ,连结
,连结 ,
, 中,
中, 分别为两腰
分别为两腰 的中点 , 确定
的中点 , 确定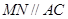 .
. 得到
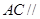 平面
平面 .
. (Ⅱ)
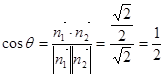 ,
, .
. 试题分析:(Ⅰ)证明:连结
 ,交
,交 与
与 ,连结
,连结 ,
, 中,
中, 分别为两腰
分别为两腰 的中点 , ∴
的中点 , ∴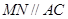 . 2分
. 2分因为
 面
面 ,又
,又 面
面 ,所以
,所以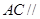 平面
平面 . 4分
. 4分(Ⅱ)解:设平面
 与
与 所成锐二面角的大小为
所成锐二面角的大小为 ,以
,以 为空间坐标系的原点,分别以
为空间坐标系的原点,分别以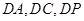 所在直线为
所在直线为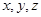 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则 ,
,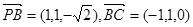 .
.设平面
 的单位法向量为
的单位法向量为 则可设
则可设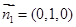 . 7分
. 7分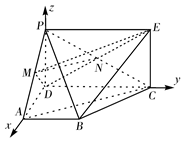
设面
 的法向量
的法向量 ,应有
,应有
即:

解得:
 ,所以
,所以 . 10分
. 10分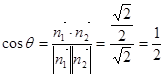 ,
, . 12分
. 12分点评:中档题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,本题利用空间向量简化了证明过程。

练习册系列答案
相关题目
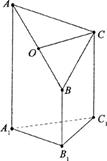
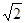 ,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.
,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.
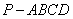 中,底面是边长为2的正方形,侧棱
中,底面是边长为2的正方形,侧棱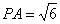 ,
,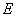 为
为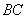 的中点,
的中点,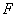 是侧棱
是侧棱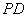 上的一动点。
上的一动点。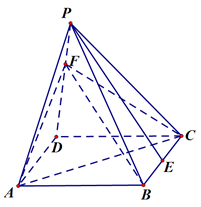
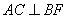 ;
;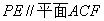 时,求三棱锥
时,求三棱锥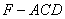 的体积.
的体积.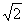 .
.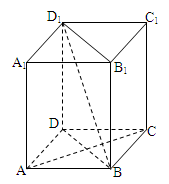
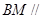 平面
平面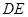 ;②
;②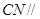 平面
平面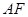 ;③平面
;③平面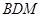
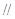 平面
平面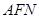 ;④平面
;④平面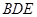
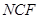 .以上四个命题中,正确命题的序号是 。
.以上四个命题中,正确命题的序号是 。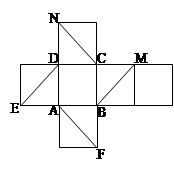
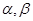 为两个不同的平面,下列四个命题中,其中正确的命题是 .(填写正确命题的序号)
为两个不同的平面,下列四个命题中,其中正确的命题是 .(填写正确命题的序号)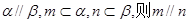 ;②若
;②若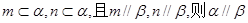 ;
;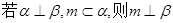 ;④
;④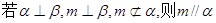
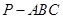 的底面
的底面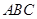 是直角三角形,且
是直角三角形,且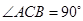 ,
,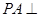 平面
平面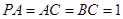 ,
,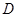 是线段
是线段 的中点,如图所示.
的中点,如图所示.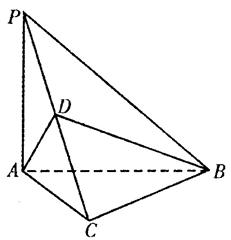
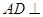 平面
平面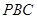 ;
;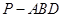 的体积.
的体积. 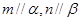 且
且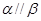 ,则
,则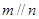 ;②若
;②若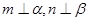 且
且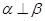 ,则
,则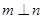 ;
; 且
且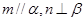 且
且 ①②
①②  ③④
③④  ①④
①④  ②③
②③